Let \(p\colon Y\rightarrow Z\) and \(f\colon X\rightarrow Z\) be continuous maps. A lifting of \(f\) to \(Y\) is a continuous map \(\widetilde{f}\colon X\rightarrow Y\) satisfying \(f=p\circ\widetilde{f}\text{.}\)
Lemma2.4.2.Uniqueness of liftings.
Let \(p\colon E\rightarrow B\) be a covering map, let \(X\) be connected, and let \(f\colon X\rightarrow Z\) be a continuous map. If \(g,h\colon Y\rightarrow Z\) are liftings of \(f\) to \(E\text{,}\) and if \(g(x_0)=h(x_0)\) for some \(x_0\in X\text{,}\) then \(g=h\text{.}\) In other words, if \(X\) is connected and \(p\colon E\rightarrow B\) is a covering map, then a lifting of \(f\) to \(E\text{,}\) if it exists, is uniquely determined by its value at any element of \(X\text{.}\)
Proof.
Assume \(g,h\) are liftings of \(f\) to \(Y\text{,}\) satisfying \(g(x_0)=h(x_0)\text{.}\) Let \(A=\{x\in X\colon g(x)=h(x)\}\subseteq X\text{.}\) We will show that \(A\) is open and closed. Since \(A\ne \emptyset\) (\(x_0\in A\)) and \(X\) is connected, it follows that \(A=X\) (1.12.5) and hence that \(g=h\text{.}\)
Take any \(x\in X\text{,}\) and let \(b=f(x)=p(g(x)=p(h(x))\text{.}\) Since \(p\) is a covering map, we can find an open neighborhood \(U\ni b\) that is evenly covered by \(p\text{.}\) Let \(p^{-1}(U)=\bigcup_{\alpha\in I}V_\alpha\) be the partition of \(p^{-1}(U)\) into slices. We will show that if \(x\in A\text{,}\) then there is an open set \(V\) with \(x\in V\subseteq A\text{;}\) and if \(x\in X-A\text{,}\) then there is an open set \(V\) with \(x\in V\subseteq X-A\text{.}\) It will follow that \(A\) is both open and closed, as desired.
Case: \(x\in A\). Since \(g(x),h(x)\in p^{-1}(b)\text{,}\) and since \(g(x)=h(x)\) (by definition of \(A\)), we have \(g(x), h(x)\in V_\alpha\) for some \(\alpha\in I\text{.}\) Consider the open set \(V=g^{-1}(V_\alpha)\cap h^{-1}(V_{\alpha})\text{.}\) We have \(x\in V\text{,}\) since \(g(x)=h(x)\in V_{\alpha}\text{.}\) Furthermore, for any \(x'\in V\text{,}\) since \(g(x'), h(x')\in V_{\alpha}\text{,}\) since \(p(g(x')=p(h(x'))=f(x')\text{,}\) and since \(p\vert_{V_{\alpha}\) is a homeomorphism, we conclude that \(g(x')=h(x')\text{.}\) Thus \(V\subseteq A\text{,}\) as desired.
Case: \(x\in X-A\). By definition of \(A\text{,}\) this means \(g(x)\ne h(x)\text{.}\) Since \(g(x),h(x)\in p^{-1}(\{b\})\text{,}\) there are \(\alpha, \alpha'\) such that \(g(x)\in V_\alpha\text{,}\)\(h(x)\in V_{\alpha'}\) and \(V_\alpha\cap V_{\alpha'}=\emptyset\text{.}\) Let \(V=g^{-1}(V_{\alpha})\cap h^{-1}(V_{\alpha'})\text{.}\) This is an open set containing \(x\text{,}\) and for all \(x'\in V\) we have \(g(x')\in V_{\alpha}\) and \(h(x')\in V_{\alpha'}\text{.}\) Since \(V_\alpha\cap V_{\alpha'}=\emptyset\text{,}\) we have \(g(x')\ne h(x')\text{.}\) Thus \(V\subseteq X-A\text{.}\)
Theorem2.4.3.Lifting to covering spaces.
Let \(p\colon E\rightarrow B\) be a covering map. Fix \(e_0\in E\) and let \(b_0=p(e_0)\text{.}\)
Every path \(f\colon I\rightarrow B\) satisfying \(f(0)=b_0\) lifts uniquely to a path \(\widetilde{f}\colon I\rightarrow E\) satisfying \(\widetilde{f}(0)=e_0\text{.}\)
Every continuous map \(F\colon I\times I\rightarrow B\) satisfying \(F(0,0)=b_0\) lifts uniquely to a continuous map \(\widetilde{F}\colon I\times I\rightarrow E\) satisfying \(\widetilde{F}(0,0)=e_0\text{.}\) Furthermore, if \(F\) is a path homotopy, then \(\widetilde{F}\) is a path homotopy.
Let \(f,g\in P(B; b_0, b_1)\text{,}\) and let \(\widetilde{f}, \widetilde{g}\) the corresponding liftings to \(E\) satisfying \(\widetilde{f}(0)=\widetilde{g}(0)=e_0\text{.}\) If \(f\simeq_p g\text{,}\) then \(\widetilde{f}\simeq_p \widetilde{g}\text{.}\)
Proof of (1).
Uniqueness of the lifting follows from Lemma 2.4.2. We now prove that there is such a lifting.
Let \(\{U_\alpha\}_{\alpha\in I}\) be a cover of \(B\) by open sets evenly covered by \(p\text{.}\) Since \(\{f^{-1}(U_\alpha)\}_{\alpha\in I}\) is an open cover of the compact metric space \(I\text{,}\) the existence of a Lebesgue number ensures that we can find a subdivision of \(I\)
that is fine enough to ensure that for all \(1\leq k\leq n\text{,}\) we have \(f([s_{k-1}, s_k])\subseteq U_{\alpha_k}\) for some \(\alpha_k\in I\text{.}\)
We now show by induction that for all \(0\leq k\leq n\text{,}\) the restriction \(f\vert_{[0,s_{k}]}\) has a lifting \(\widetilde{f}_k\colon [0,s_k]\rightarrow E\) satisfying \(\widetilde{f}_k(0)=e_0\text{.}\) It will follow that \(\widetilde{f}=\widetilde{f}_n\colon [0,1]\rightarrow E\) is the lifting we are after.
Base case: \(k=0\). The function \(\widetilde{f}_0\colon \{0\}\rightarrow E\text{,}\) defined as \(\widetilde{f}_0(0)=e_0\) is a lifting of \(f_0\text{.}\)
Induction step. Assume \(\widetilde{f}_k\colon [0,s_k]\rightarrow E\) is a lifting of \(f\vert_{[0,s_k]}\) satisfying \(\widetilde{f}_k(0)=e_0\text{.}\) Recall that we have \(f([s_k, s_{k+1}])\subseteq U\) for some open set evenly covered by \(p\text{.}\) Let \(p^{-1}(U)=\bigcup_{\beta\in J} V_{\beta}\text{.}\) Since \(\widetilde{f}_k(s_k)\in p^{-1}(U)\text{,}\) there is a unique slice \(V=V_\beta\) in this partition containing \(\widetilde{f}_k(s_k)\text{.}\) Since \(p\vert_V\) is a homeomorphism, we can define a continuous function \(g\colon [s_k, s_{k+1}]\colon V\) as \(g=(p\vert_V)^{-1}\circ f\text{.}\) Since \(p\) is 1-1 on \(V\) and since \(p(\widetilde{f}_k(s_k))=p(g(s_k))=f(s_k)\text{,}\) we have \(\widetilde{f}_k(s_k)=g(s_k)\text{.}\) By the closed pasting lemma, the function \(\widetilde{f}_{k+1}\colon [0,s_{k+1}]\rightarrow E\) defined as
is continuous. That \(\widetilde{f}_{k+1}\) is a lifting of \(f\vert_{[0,s_{k+1}]}\) satisfying \(\widetilde{f}_{k+1}(0)=e_0\) follows from the assumed properties of \(\widetilde{f}_k\) and the definition of \(g\) as \((p\vert_V)^{-1}\circ f\text{.}\)
Proof of (2).
The argument here is essentially isomorphic to the one given above, though some minor subtleties creep in due to the slightly more complex domain in play (\(I\times I\) as opposed to \(I\)). Note first that once again the uniqueness property described follows immediately from Lemma 2.4.2.
Let \(\{U_{\alpha}\}_{\alpha\in I}\) be a cover of \(B\) by open sets evenly covered by \(p\text{.}\) Since \(I\times I\) is compact, the open cover \(\{F^{-1}(U_{\alpha)\}_{\alpha\in I}\) has a Lebesgue number\(\delta\text{.}\) Pick a subdivision of \(I\)
fine enough so that the diameter of each subrectangle \(R_{k,l}=[s_{k-1}, s_k]\times [s_{l-1}, s_{l}]\) in the resulting subdivision of \(I\times I\) is less than \(\delta\text{.}\) It follows that for all \(1\leq k,l\leq n\) we have \(F(R_{k,l})\subseteq U_\alpha\) for some \(\alpha\in I\text{.}\)
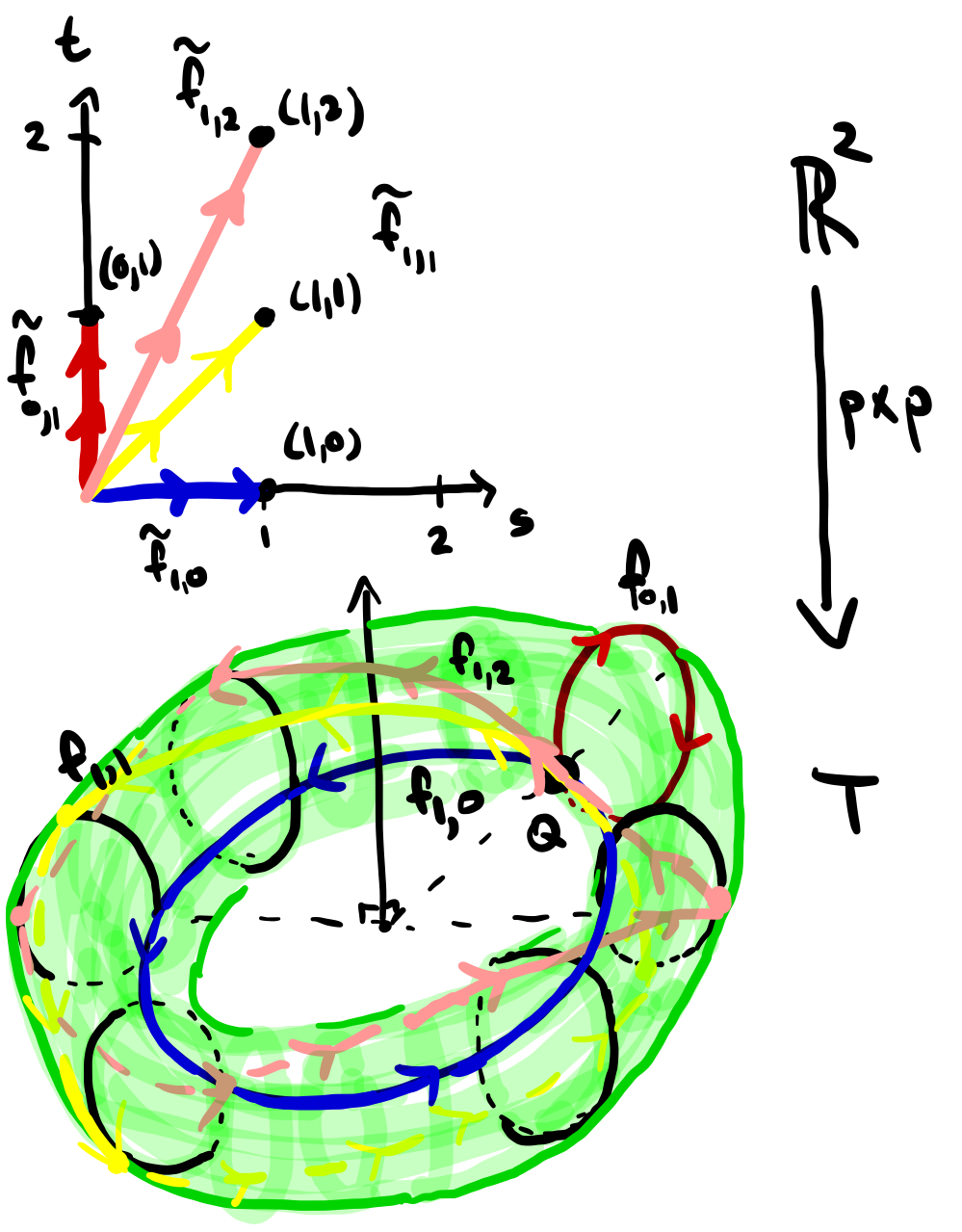
We now endeavor to build a lifting of \(F\) subrectangle by subrectangle, from the bottom row of subrectangles to the top, working from left to right along each row. In more detail for each pair \(1\leq k,l\leq n\) let the region \(A_{k,l}\) be the union of the rectangle \(R_{k,l}\) along with all rectangles \(R_{i,j}\) to the left or below it. We will show by induction that for all \(1\leq k,l\leq n\) there is a lifting \(\widetilde{F}_{k,l}\colon A_{k,l}\rightarrow E\) of \(F\vert_{A_{k,l}}\) satisfying \(\widetilde{F}_{k,l}(0,0)=e_0\text{.}\) Since \(I\times I=A_{n,n}\) the lifting \(\widetilde{F}=\widetilde{F}_{n,n}\) gives us what we want.
Base case. We have \(A_{1,1}=R_{1,1}\text{,}\) the lower left corner of \(I\times I\text{.}\) By construction, we have \(F(R_{1,1})\subseteq U\text{,}\) where \(U\) is an open set evenly covered by \(p\text{.}\) Let \(p^{-1}(U)=\bigcup_{\beta\in J}V_\beta\) be the corresponding partition into slices, and let \(V=V_{\beta}\) be the slice containing \(f(0,0)=e_0\text{.}\) Define \(\widetilde{f}_{1,1}\colon A_{1,1}=R_{1,1}\rightarrow E\) as \(\widetilde{F}_{1,1}=(p\vert_V)^{-1}\circ f\text{.}\) It is easy to see that \(p\circ \widetilde{F}_{1,1}(s,t)=F(s,t)\) for all \((s,t)\in A_{1,1}=R_{1,1}\text{.}\) Since \(p\) is 1-1 on \(V\) and \(p(\widetilde{F}(0,0))=p(e_0)=b_0\text{,}\) we see that \(\widetilde{F}_{1,1}(0,0)=e_0\text{.}\)
Induction step. Pick any pair \(1\leq k,l\leq n\) with \((k,l)\ne (n,n)\) and assume that \(\widetilde{F}_{k,l}\) is a lifting of \(F\vert_{A_{k,l}}\) that satisfies \(\widetilde{F}_{k,l}(0,0)=e_0\text{.}\) The “next” region in our procedure is either (a) \(A_{k+1,l}=A_{k,l}\cup R_{k+1,l}\) if \(k\ne n\) (“move to right if you can”), or (b) \(A_{1,l+1}=A_{n,l}\cup R_{1,l+1}\) (“move up a row and start at left”). We show in case (a) that we can extend \(\widetilde{F}_{k,l}\) to this larger region; the argument for case (b) is very similar.
In case (a) we have \(A_{k+1,l}=A_{k,l}\cup R_{k+1,l}\text{.}\) Let
a connected set formed as the union of the left and bottom edges of \(R_{k+1, l}\text{.}\) By construction we have \(F(R_{k+1,l})\subseteq U \) for some open set evenly covered by \(p\text{.}\) Let \(p^{-1}(U)=\bigcup_{\beta\in J} V_{\beta}\) be its partition into slices. Since \(C\subseteq A_{k,l}\) and \(C\) is connected, we must have \(\widetilde{F}_{k,l}(C)\subseteq V_\beta\) for one of the slices \(V=V_\beta\text{.}\) (Otherwise we would have a separation of the connected set \(\widetilde{F}_{k,l}(C)\text{.}\)) Define \(g\colon R_{k+1,l}\rightarrow E\) as \(g=(p\vert_V)^{-1}\circ F\text{.}\) Arguments very similar to the ones in the previous proof show that \(g\vert_C=\widetilde{F}_{k,l}\vert_C\) and thus the two functions can be pasted together to form the desired lifting \(\widetilde{F}_{k+1,l}\) of \(F\vert_{A_{k+1,l}}\text{.}\)
Lastly we show that if \(F\) is a path homotopy, then \(\widetilde{F}\) is a path homotopy. Assume \(F(0,t)=b_0\) and \(F(1,t)=b_1\) for all \(t\in I\text{.}\) We have \(\widetilde{F}(0,0)=e_0\in p^{-1}(\{b_0\})\) by assumption; let \(e_1=\widetilde{F}(1,0)\in p^{-1}(\{b_1\})\text{.}\) We must show that \(\widetilde{F}(0,t)=e_0\) and \(\widetilde{F}(1,t)=e_1\) for all \(t\in I\text{.}\) Let \(H(t)=\widetilde{F}(0,t)\text{.}\) This is a continuous function from \(I\) to the preimage \(p^{-1}(\{b_0\})\text{.}\) Since its image is connected, and since \(p^{-1}(\{b_0\})\) is discrete, this image must be a singleton. Since \(H(0)=\widetilde{F}(0,0)=e_0\)We conclude that \(H(t)=\widetilde{F}(0,t)=e_0\) for all \(t\in I\text{.}\) A similar argument, using \(H(t)=\widetilde{F}(1,t)\) shows that \(\widetilde{F}(1,t)=e_1\) for all \(t\in I\text{.}\)
Proof of (3).
Assume \(f\simeq_p g\) and let \(F\colon I\times I\rightarrow B\) be the path homotopy that witnesses this fact. From (2) we know that \(F\) lifts uniquely to a path homotopy \(\widetilde{F}\colon I\times I\rightarrow B\) satisfying \(\widetilde{F}(0,t)=e_0\) for all \(t\in I\text{.}\) Since \(\widetilde{F}\) is a lifting of \(F\text{,}\) we have \(p(\widetilde{F}(s,0))=F(s,0)=f(s)\) and \(p(\widetilde{F}(s,1))=F(s,1)=g(s)\text{.}\) Thus the paths \(\hat{f}(s)=\widetilde{F}(s,0)\) and \(\hat{g}(s)=\widetilde{F}(s,1)\) are liftings of \(f\) and \(g\) to \(E\text{.}\) Since \(\hat{f}(0)=\widetilde{F}(0,0)=e_0\) and \(\hat{g}(0)=\widetilde{F}(0,1)=e_0\text{,}\) we conclude from the uniqueness property of liftings that \(\hat{f}(s)=\widetilde{F}(s,0)=\widetilde{f}(s)\) and \(\hat{g}(s)=\widetilde{F}(s,1)=g(s)\text{,}\) as desired.
Definition2.4.4.Lifting correspondence.
Let \(p\colon E\rightarrow B\) be a covering map. Fix \(e_0\in E\) and let \(b_0=p(e_0)\text{.}\) The function
where \(\widetilde{f}\) is the unique lifting of \(f\) to \(E\) satisfying \(\widetilde{f}(0)=e_0\text{,}\) is called the lifting correspondence arising from the covering \(p\) and choice of \(e_0\in E\text{.}\)
Proof.
The fact that the rule \([f] \mapsto \widetilde{f}(1)\) gives rise to a well-defined function of sets follows from Theorem 2.4.3
Statement (1) of this theorem guarantees the existence and uniqueness of \(\widetilde{f}\text{.}\) Note also that since \(p(\widetilde{f}(1))=f(1)=b_0\text{,}\) the value \(\widetilde{f}(1)\) is indeed an element of \(p^{-1}(\{b_0\})\text{.}\)
Statement (3) of the theorem ensures that if \([f]=[g]\in \pi_1(B,b_0)\text{,}\) then \(\widetilde{f}(1)=\widetilde{g}(1)\text{.}\) Indeed, since \(f\simeq_p g\text{,}\) we conclude that \(\widetilde{f}\simeq_p \widetilde{g}\text{.}\) In particular, being path homotopic, we must have \(\widetilde{f}(1)=\widetilde{g}(1)\text{.}\)
Theorem2.4.5.Lifting correspondence.
Let \(p\colon E\rightarrow B\) be a covering map. Fix \(e_0\in E\text{,}\) let \(b_0=p(e_0)\text{,}\) and let
Furthermore the map \(\overline{\phi}\) is bijective if \(E\) is path connected.
Proof of (1).
Since \(p^*\) is a group homomorphism, to show it is injective it suffices to show that \(\ker p^*=\{e\}=\{[e_{e_0}]\}\text{.}\) (Recall that the identity element of a fundamental group \(\pi_1(X,x_0)\) is \(e=[e_{x_0}]\text{.}\)) To this end, suppose \([f]\in \pi_1(E,e_0)\) satisfies \(p_*([f])=[\pi\circ f]=[e_{b_0}]\in \pi_1(B,b_0)\text{.}\) It follows from the uniqueness property of liftings that \(f=\widetilde{p\circ f}\) and \(e_{e_0}=\widetilde{e_{b_0}}\text{.}\) Since \(p\circ f\simeq_p e_{b_{0}\text{,}\) it follows from (3) of Theorem 2.4.3 that \(f\simeq_p e_{e_0}\text{,}\) and thus \([f]=[e_{e_0}]\text{.}\) This proves that if \(p_*([f])=e \text{,}\) then \([f]=e\text{:}\) i.e., \(\ker p_*=\{e\}\text{.}\)
Proof of (2).
We prove both implications separately.
Implication: \(\Rightarrow\). Assume \(\phi([f])=e_0\text{.}\) By definition of \(\phi\) this means the unique lifting \(\widetilde{f}\) satisfying \(\widetilde{f}(0)=e_0\) also satisfies \(\widetilde{f}(1)=e_0\text{.}\) Thus \(\widetilde{f}\in P(E; e_0,e_0)\text{,}\) and we have \(p_*[\widetilde{f}]=[p\circ \widetilde{f}]=[f]\text{.}\) Thus \([f]\in \im p_*=H\text{.}\)
Implication: \(\Leftarrow\). If \([f]\in \im p_*\text{,}\) then \([f]=[p\circ g]\) for some \(g\in P(E; e_0, e_0)\text{.}\) As argued in (1), we have \(g=\widetilde{p\circ g}\text{.}\) Thus \(\phi([f])=\phi([p\circ g])=g(1)=e_0\text{.}\)
Proof of (3).
First observe that if \(E\) is path connected, then given any \(e'\in p^{-1}(\{b_0\}\text{,}\) there is a path \(f\in P(E;e_0,e')\text{.}\) Since \(f=\widetilde{p\circ f}\text{,}\) we have \(\phi([p\circ f])=\widetilde{p\circ f}(1)=f(1)=e'\text{,}\) and thus \(e'\in \im \phi\text{.}\) We conclude that \(\phi\) (and \(\overline{\phi}\)) are surjective in this case.
Next, we show that if \(\phi([f])=\phi([g])\text{,}\) then \([f]\in H*[g]\text{.}\) Let \(\widetilde{f}, \widetilde{g}\) be the unique liftings of \(f, g\) satisfying \(\widetilde{f}(0)=\widetilde{g}(0)=e_0\text{.}\) Since \(\phi([f])=\widetilde{f}(1)\) and \(\phi([g])=\widetilde{g}(1)\text{,}\) the assumption \(\phi([f])=\phi([g])\) is equivalent to \(\widetilde{f}(1)=\widetilde{g}(1)=e_1\) for some common element \(e_1\in p^{-1}(\{b_0\}\text{.}\) Let \(\overline{\widetilde{g}}\) be the reverse of \(\widetilde{g}\text{.}\) Since this begins where \(\widetilde{f}\) ends, we can take the path product \(\widetilde{f}*\overline{\widetilde{g}}\text{,}\) which is an element of \(P(E; e_0,e_0)\text{.}\) Now we have
It follows that \([h]=p_*([\widetilde{f}*\overline{\widetilde{g}}])\in H\text{.}\) Since \([h]=[f]*[\overline{g}]=[f]*[g]^{-1}\text{,}\) we have \([f]=[h]*[g]\in H*[g]\text{,}\) as desired.
Lastly, assume \([f]\in H*[g]\text{,}\) in which case \([f]=[h]*[g]=[h*g]\) for some \(h=p\circ q\text{,}\) where \(q\in P(E; e_0, e_0)\text{.}\) We see easily that \(q*g\) is well-defined (in terms of the path product) and the usual uniqueness argument shows \(q*g=\widetilde{h*g}\text{.}\) We conclude that
Consider the covering \(p\colon \R\rightarrow S^1\) defined as \(p(s)=(\cos 2\pi s, \sin 2\pi s)\text{.}\) Let \(Q=(1,0)\) and consider the map \(p_*\colon \pi_1(\R, 0)\rightarrow \pi_1(S^1, Q)\text{.}\) Since \(\R\) is path connected, and since \(\pi_1(\R, 0)\) is trivial, we have \(H=p_*(\pi_1(X,0))=\{e\}\text{,}\) and it follows from (3) of Theorem 2.4.5 that the lifting correspondence \(\phi\colon \pi_1(S^1, Q)\rightarrow p^{-1}(Q)\) is a bijection onto \(p^{-1}(Q)=\Z\text{.}\)
We will show that \(\phi\) is in fact a group homomorphism hence an isomorphism, but before we do, it is worth making the bijective correspondence between \(\pi_1(S^1, Q)\) and \(\Z\) more explicit. Consider the family of loops \(\{f_n\}_{n\in \Z}\) defined as \(f_n(s)=(\cos 2\pi n s, \sin 2\pi n s)\text{.}\) Note that \(f_n\) is a path that traverses the circle \(n\) complete times traveling counterclockwise if \(n> 0\) and clockwise if \(n< 0\text{.}\) By Theorem 2.4.3 the paths \(f_n\) lift uniquely to paths \(\widetilde{f}_n\) satisfying \(\widetilde{f}_n(0)=0\text{.}\) We see easily that \(s\mapsto ns\) is such a lifting for each \(n\text{;}\) uniqueness then implies that \(\widetilde{f}_n(s)=ns\) for all \(n\in \Z\text{.}\) The liftings \(\widetilde{f}_n\) are just the usual straight line segment parametrizations from \(0\) to \(n\text{,}\) and thus the lifting correspondence applied to \([f_n]\) is \(\phi([f_n])=\widetilde{f}_n(1)=n\text{.}\) The bijective nature of \(\phi\) now implies that \([f_m]\ne [f_n]\) for\(m\ne n\text{,}\) and that
In other words every loop in \(S^1\) is path homotopic to \(f_n\) for a unique choice of \(n\text{.}\)
To show \(\phi\) is a group homomorphism it now suffices to show that \(\phi([f_m]*[f_n])=\phi([f_m])+\phi([f_n])=m+n\text{.}\) To do so we explicitly identify the unique lifting of \(f_m*f_n\text{.}\) You might have guessed that \(\widetilde{f}_m*\widetilde{f}_n\) would do the trick, but notice that this path product is not even well defined since \(\widetilde{f}_m\) ends at \(m\text{,}\) and \(\widetilde{f}_n\) begins at 0. This is easily remedied by replacing \(\widetilde{f}_n\) with the function \(t_m\circ \widetilde{f}_n\text{,}\) where \(t_m(x)=x+m\) is the translation by \(m\) operation on \(\R\text{.}\) Let \(h=\widetilde{f}_m*(t_m\circ \widetilde{f}_n)\text{.}\) Since \(h(0)=0\) and
let \(Q=p\times p(0,0)=\left((1,0),(1,0)\right)\in T\text{.}\) As in the previous example, it follows easily from (3) of Theorem 2.4.5 that the lifting correspondence associated to the map of pointed sets \(p\times p\colon (\R\times \R, (0,0))\rightarrow (T, Q)\) is a bijection
Consider the family of loops \(\{f_{m,n}\}_{(m,n)\in \Z\times \Z}\) defined as
\begin{equation*}
f_{m,n}(s)=(f_m(s),f_n(s))=\left((\cos 2\pi m s, \sin 2\pi m s), (\cos 2\pi n s, \sin 2\pi n s)\right)\text{.}
\end{equation*}
You find a sketch of some of these loops (and their lifts) in Figure 2.4.8, where I have identified \(S^1\times S^1\) with an embedded surface of \(\R^3\) in the usual way.
As in Example 2.4.6, it is easy to see that for all \((m,n)\in \Z\times \Z\) we have
which is the usual line segment parametrization from \((0,0)\) to \((m,n)\text{.}\) We conclude that \(\phi([f_{m,n}]=(m,n)\text{,}\) from whence it follows that all loops in \(T\) starting and ending at \(Q\) are homotopic to \(f_{m,n}\) for a unique pair \((m,n)\in \Z\times \Z\text{.}\) This fact is useful in its own right, but also allows us to show that \(\phi\) is in fact a group homomorphism, and hence an isomorphism. The proof proceeds in exactly the same manner as with Example 2.4.6: again, the only subtlety is finding the unique lift of \(f_{m,n}*f_{k,l}\) for any two pairs \((m,n), (k,l)\in \Z\times \Z\text{.}\) This lift turns out to be \(\widetilde{f}_{m,n}*(t_{(m,n)}\circ \widetilde{f}_{k,l})\text{,}\) where \(t_{(m,n)}(x,y)=(x+m, y+n)\) is the translation by \((m,n)\) operation on \(\R\times \R\text{.}\)
Figure2.4.8.Some loops on the torus and their lifts
