Volume via cross sections

Section 1.9 Volume via cross sections

In our discussion of area of regions in \(\R^2\text{,}\) we started with basic area formulas (rectangles) and investigated how we could use these basic formulas to estimate the area of more general regions via Riemann sums. This in turn motivated our definition of our area via the integral, which we understood as the limit of these estimates as they get more and more accurate. In the end we used the integral to produce a more general notion of area that could be applied to more interesting regions.

We will now take a similar approach to defining the volume of a solid region \(\mathcal{S}\subseteq \R^3\) in three-space. The rough outline of our approach is meant to bring out the similarities between the two approaches.

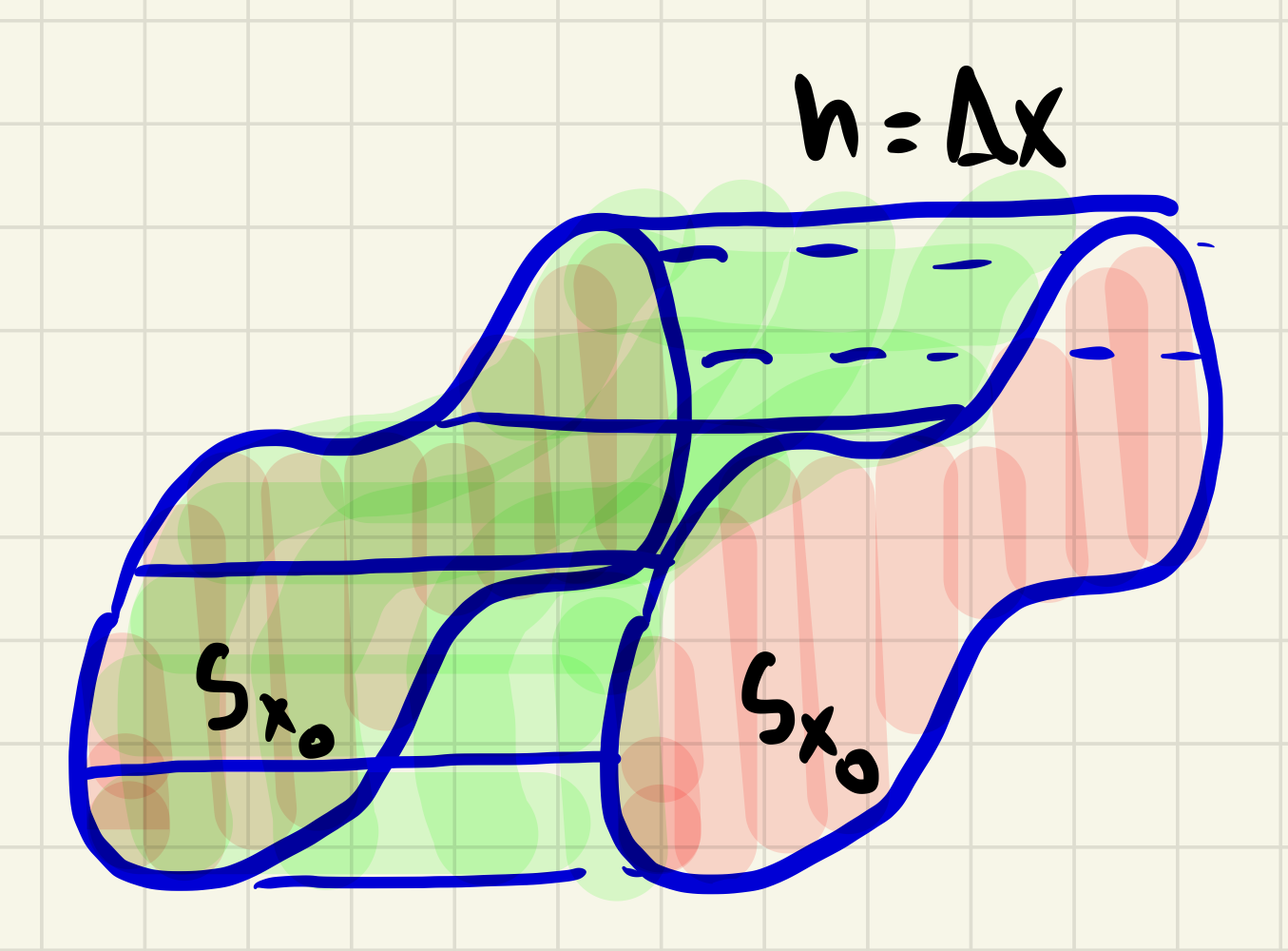
Begin with a set of basic volume formulas assumed to be true. We will start with the volume formula \(V=A\cdot h\) for a solid cylinder of general base of area \(A\text{,}\) and height \(h\text{.}\)
Estimate the volume of a general region by approximating it as a union of such general cylinders and summing up their volumes.
Define the volume of the region to be the limit of these estimates and identify this limit as the integral of a certain function.

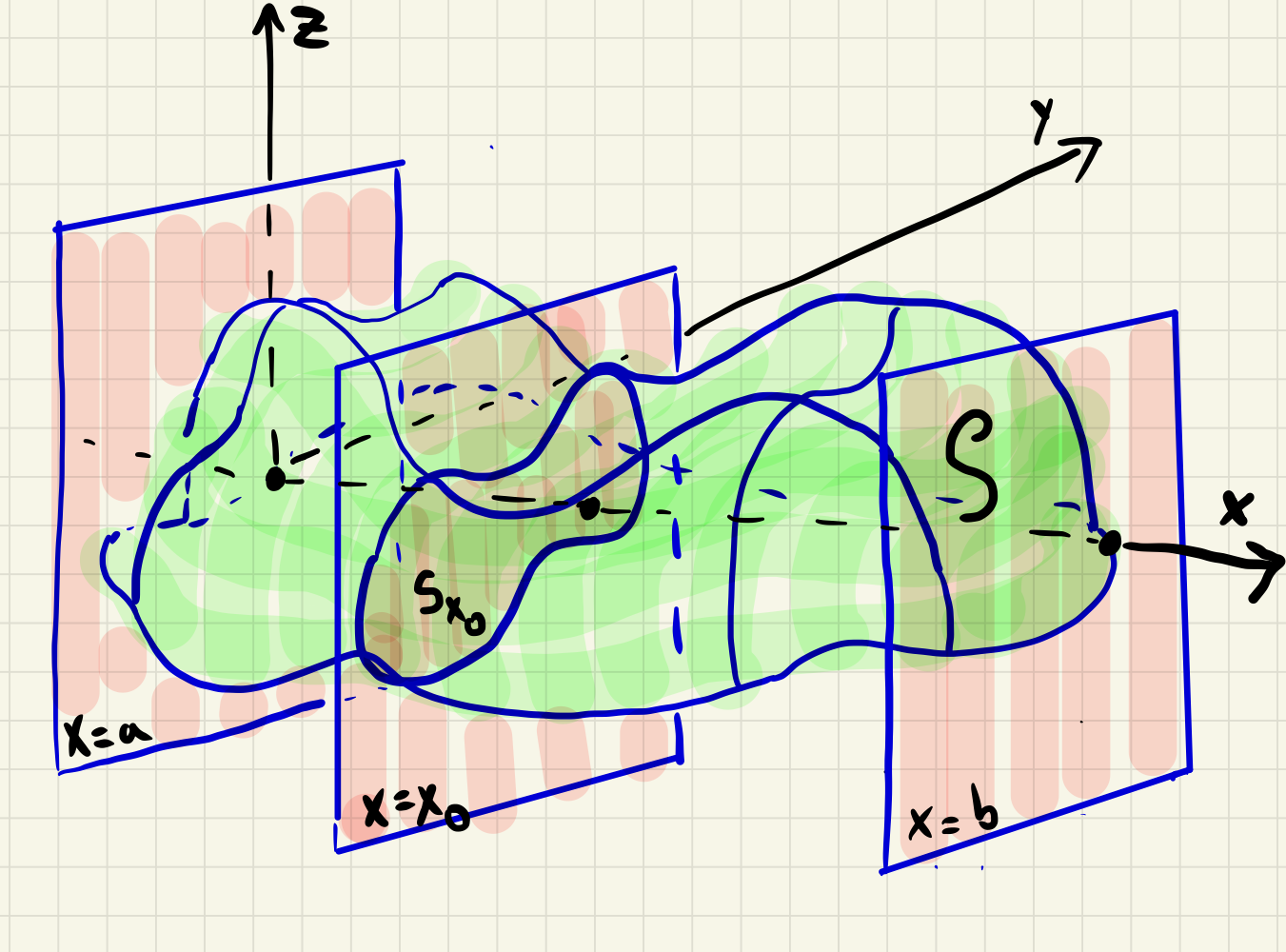
In more detail, imagine our solid \(\mathcal{S}\) lying in \(\R^3\) and choose a coordinate system with the \(x\)-axis running through \(\mathcal{S}\text{.}\) Imagine slicing \(\mathcal{S}\) up with many vertical planes oriented perpendicularly to the \(x\)-axis. Assume the solid \(\mathcal{S}\) lies entirely between the planes \(x=a\) and \(x=b\text{.}\)

For any fixed \(x=x_0\text{,}\) the vertical plane \(x=x_0\) intersected with \(\mathcal{S}\) yields a cross section \(S_{x_0}\) of \(\mathcal{S}\) that we call the \(x=x_0\)-cross section.

A cross section of the solid \(\mathcal{S}\)
We approximate the portion of \(\mathcal{S}\) located between two planes planes \(x=x_0\) and \(x=x_0+\Delta x\) as a general cylinder with base \(\mathcal{S}_{x_0}\) and height \(\Delta x\text{.}\) Let \(A(x_0)=\operatorname{area} S_{x_0}\text{.}\) The volume of this cylinder is given by

\begin{equation*} V=A(x_0)\cdot \Delta x\text{,} \end{equation*}

and we consider this an approximation of the volume of this portion of \(\mathcal{S}\text{.}\)

Volume of general cylinder\(\mathcal{S}\)
Recall that \(\mathcal{S}\) lies entirely between the planes \(x=a\) and \(x=b\text{.}\) To estimate the volume of \(\mathcal{S}\) we partition \([a,b]\) into \(n\) equal subintervals

\begin{equation*} a=x_0\lt x_1\lt \dots \lt x_n=b \end{equation*}

and approximate the volume of the portion of \(\mathcal{S}\) between \(x_k\) and \(x_{k+1}\) as \(A(x_k)\Delta x\text{,}\) as above. The sum of these approximations yields an approximation of the volume of \(\mathcal{S}\text{:}\)

\begin{align*} \operatorname{vol} S\amp \approx A(x_0)\Delta x+A(x_1)\Delta x+\cdots A(x_{k-1})\Delta X \\ \amp = \sum_{k=1}^n A(x_{k-1})\Delta x\text{.} \end{align*}

We recognize this expression as the \(n\)-th left Riemann summ of the cross section area function \(A(x)\) on the interval \([a,b]\text{.}\)
Taking the limit of these approximations as \(n\to \infty\) should yield the exact volume of \(\mathcal{S}\text{.}\) Thus we define

\begin{align*} \operatorname{vol} S \amp =\lim_{n\to\infty}\sum_{k=1}^n A(x_{k-1})\Delta x \\ \amp = \int_a^b A(x)\, dx\text{.} \end{align*}

Definition 1.9.1. Volume via cross sections.

Let \(\mathcal{S}\subseteq \R^3\) be a solid region in \(3\)-space lying between the planes \(x=a\) and \(x=b\text{.}\) For each \(x\in [a,b]\) let \(\mathcal{S}_{x}\) be the corresponding \(x\)-cross section of \(\mathcal{S}\) and let \(A(x)\) be the area of \(S_{x}\text{.}\)

Assume \(A(x)\) is integrable on the interval \([a,b]\text{.}\) We define the volume \(\operatorname{vol}\mathcal{S}\) of \(\mathcal{S}\) as

\begin{equation} \operatorname{vol}\mathcal{S}=\int_a^b A(x)\, dx\text{.}\tag{1.9.1} \end{equation}

The volume of \(\mathcal{S}\) can be defined with respect to any linear axis (e.g., the \(y\)- or \(z\)-axis) using an analogous formula to (1.9.1).

Procedure 1.9.2. Volume via cross sections.

To compute the volume of a solid region \(\mathcal{S}\) via \(x\)-cross sections, proceed as follows:

Sketch \(\mathcal{S}\) along with a typical cross section \(\mathcal{S}_x\text{.}\)
Derive a formula for \(A(x)\) in terms of \(x\text{.}\)
Determine the appropriate limits of integration: \(x=a\) and \(x=b\text{.}\)
Compute \(\displaystyle \int_a^b A(x)\, dx\text{.}\)

Example 1.9.3. Volume of sphere.

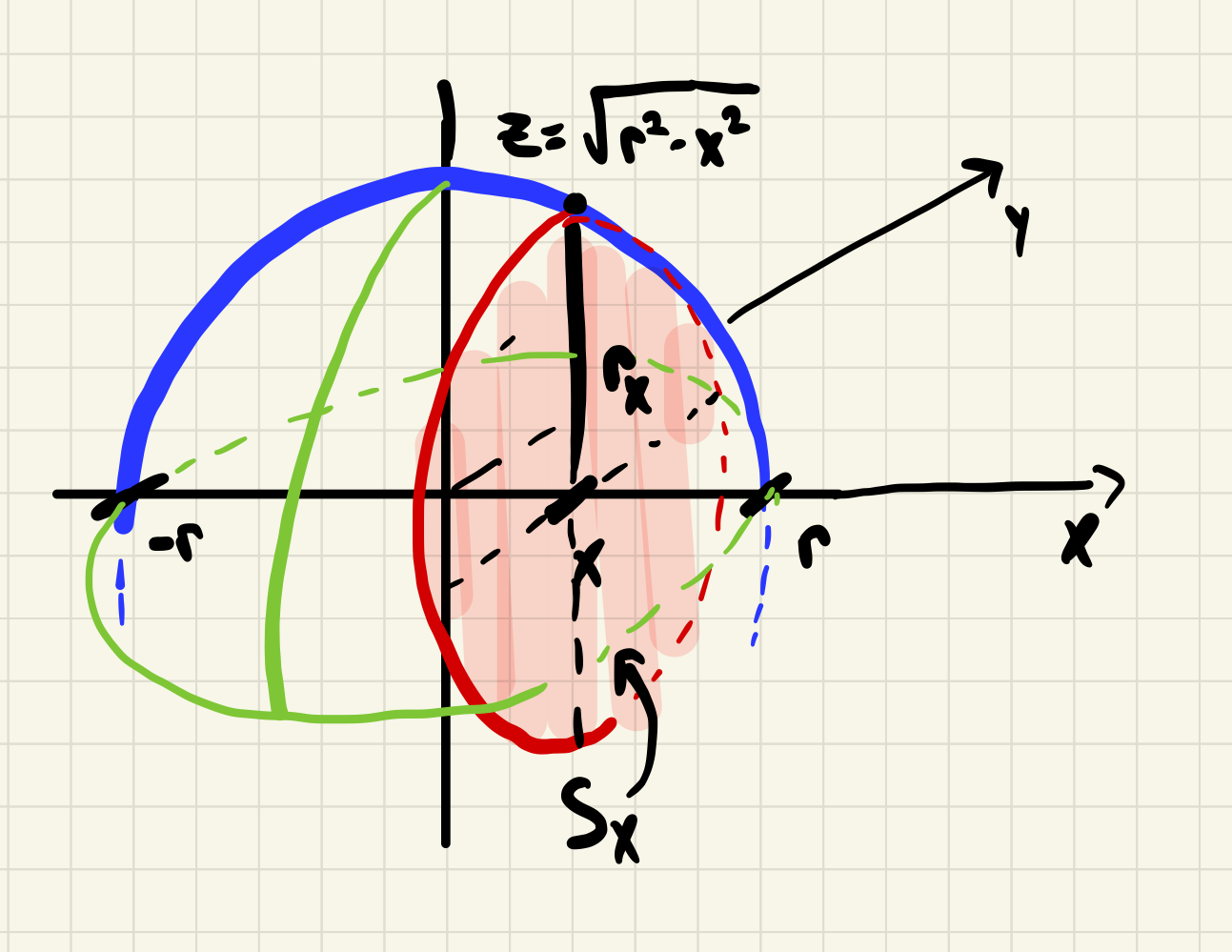
Let \(\mathcal{S}\) be the solid sphere centered at the origin of radius \(r\text{.}\) Compute \(\operatorname{vol}\mathcal{S}\) using cross sections.

Solution.

As the diagram below illustrates, each \(x\)-cross section \(S_x\) of the sphere \(\mathcal{S}\) is a circle of radius \(r_x=\sqrt{r^2-x^2}\text{.}\) Thus

\begin{equation*} A(x)=\pi r_x^2=\pi(r^2-x^2) \end{equation*}

and

\begin{align*} \operatorname{vol}\mathcal{S} \amp = \int_{-r}^rA(x)\, dx\\ \amp = \int_{-r}^r\pi (r^2-x^2)\, dx\\ \amp = \pi(r^2x-\frac{1}{3}x^3)\Bigr\vert_{-r}^r\\ \amp = \pi(2r^3-\frac{2}{3}r^3\\ \amp = \frac{4}{3}\pi r^3 \end{align*}

as expected!

Example 1.9.4. Volume of cone.

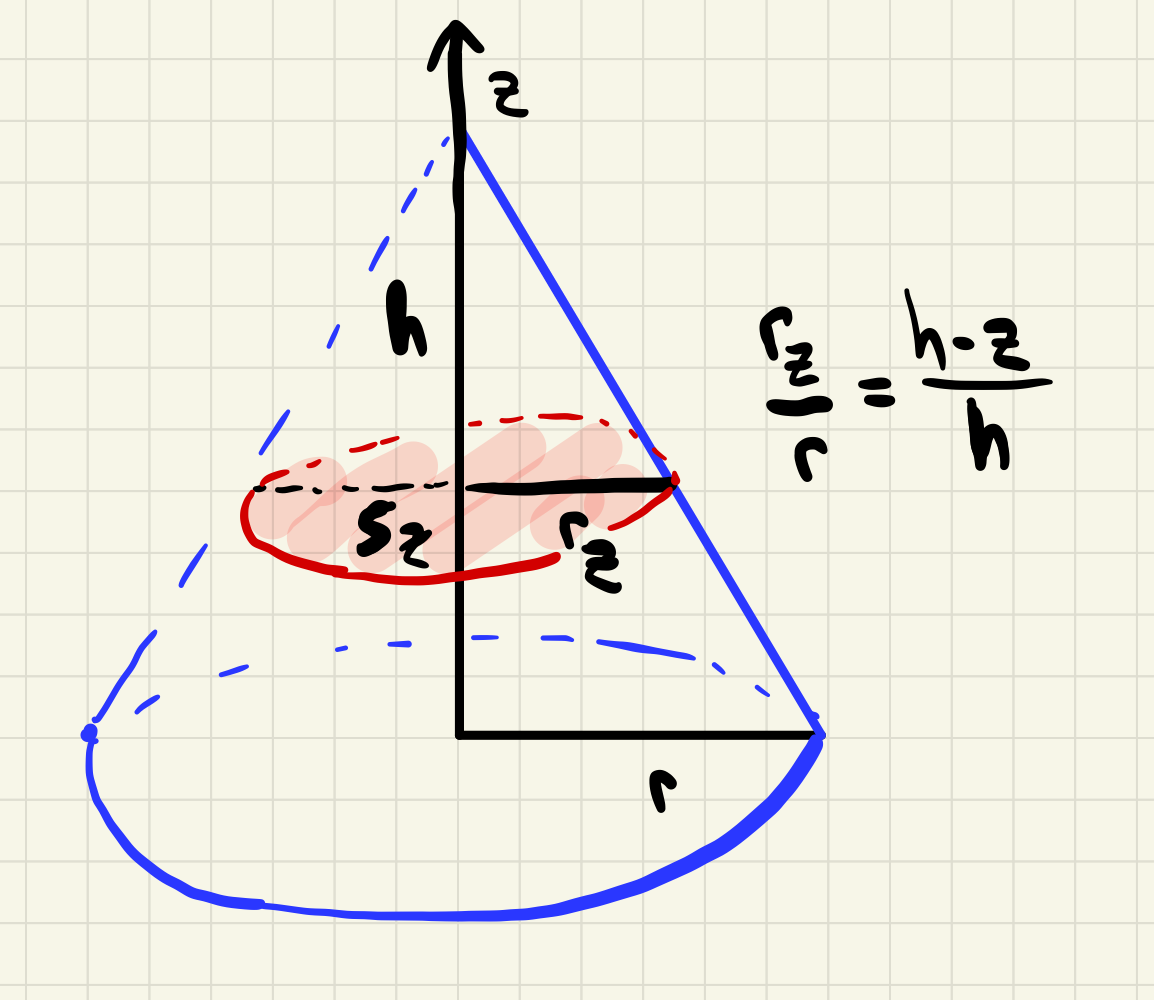
Let \(\mathcal{S}\) be the solid cone with base the disc \(D\) in the \(xy\)-plane with equation \(x^2+y^2=r^2\) and vertex \(P\) lying directly above the origin at a height of \(h\text{.}\) Compute \(\operatorname{vol} \mathcal{S}\) using cross sections.

Solution.

Picking out two similar right triangles in the diagram below, we see that each \(z\)-cross section \(S_z\) of the cone \(\mathcal{S}\) is a circle of radius \(r_z\) satisfying \(\frac{r_z}{r}=\frac{h-z}{h}\text{,}\) or \(r_z=r-\frac{r}{h}z\text{.}\) Thus

\begin{equation*} A(z)=\pi r_z^2=\pi(r-\frac{r}{h}z)^2 \end{equation*}

and

\begin{align*} \operatorname{vol}\mathcal{S} \amp = \int_{0}^hA(z)\, dz\\ \amp = \int_{0}^h\pi (r-\frac{r}{h}z)^2\, dz\\ \amp = \pi\int_r^{0}-\frac{h}{r}u^2\, du \amp (u=r-\frac{r}{h}x, du=-\frac{r}{h}dx)\\ \amp = -\frac{\pi\, h}{r}\frac{u^3}{3}\Bigr\vert_{r}^0\\ \amp = \frac{1}{3}\pi r^2 h\text{.} \end{align*}

Note that the volume of the cone is equal to one-third the volume of the cylinder of radius \(r\) and height \(h\text{!}\)

Definition 1.9.1 is quite general: it can be applied to any solid region with an integrable cross sectional area function \(A(x)\text{.}\) For the remainder of the section, we consider a very special type of solid: namely a solid of rotation.

Definition 1.9.5. Solid of revolution.

A solid of revolution is a solid region \(\mathcal{S}\subseteq \R^3\) obtained by rotating a planar region \(\mathcal{R}\) around a central linear axis \(L\text{.}\)

Solids of revolution are a very particular sort of solid region, and enjoy many symmetry properties. When computing their volumes with respect to their axis of symmetry, cross sections are often disks or washers, and thus the area cross section function \(A\) takes a particular form. The following procedure considers two typical cases; it can be applied mutatis mutandi to solids or revolution with axis of rotation parallel to the \(y\)- or \(z\)-axis.

Procedure 1.9.6. Volume of solid of revolution.

In each case below, let \(\mathcal{S}\) be the solid of revolution obtained by rotating the given region \(\mathcal{R}\) around the given line \(L\text{.}\)

Disks.
Let \(L\) be the line \(y=c\text{,}\) and let \(f\) be an integrable function on the interval \([a,b]\) satisfying \(f(x)\geq c\) for all \(x\in [a,b]\text{.}\) Define \(\mathcal{R}\) to be the region in the \(xy\)-plane lying between the graph of \(f\) and \(L\text{,}\) and between the lines \(x=a\) and \(x=b\text{.}\)
- For all \(x\in [a,b]\) the cross section \(\mathcal{S}_x\) is a disk of radius \(r_x=f(x)-c\text{.}\)
- The cross sectional area function of \(\mathcal{S}\) is thus given by
  
  \begin{equation} A(x)=\pi(f(x)-c)^2\text{.}\tag{1.9.2} \end{equation}
- The volume of \(\mathcal{S}\) is thus
  
  \begin{equation} \operatorname{vol}\mathcal{S}=\int_a^b\pi (f(x)-c)^2\, dx\text{.}\tag{1.9.3} \end{equation}
Washers.
Let \(L\) be the line \(y=c\text{,}\) and let \(f\) and \(g\) be integrable functions on the interval \([a,b]\) satisfying \(f(x)\geq g(x)\geq c\) for all \(x\in [a,b]\text{.}\) Define \(\mathcal{R}\) to be the region in the \(xy\)-plane lying between the graphs of \(f\) and \(g\text{,}\) and between the lines \(x=a\) and \(x=b\text{.}\)
- For all \(x\in [a,b]\) the cross section \(\mathcal{S}_x\) of \(\mathcal{S}\) is a washer of inner radius \(r_x=g(x)-c\) and outer radius \(R_x=f(x)-c\text{.}\)
- The cross sectional area function of \(\mathcal{S}\) is thus given by
  
  \begin{equation} A(x)=\pi((f(x)-c)^2-(g(x)-c)^2)\text{.}\tag{1.9.4} \end{equation}
- The volume of \(\mathcal{S}\) is
  
  \begin{equation} \operatorname{vol}\mathcal{S}=\int_a^b\pi((f(x)-c)^2-(g(x)-c)^2)\, dx\text{.}\tag{1.9.5} \end{equation}

Example 1.9.7. Disk example.

Let \(f(x)=5-\frac{3}{7}x\text{,}\) let \(\mathcal{R}\) be the region in the first quadrant lying below the graph of \(f\) and above the line \(L\) with equation \(y=2\text{,}\) and let \(\mathcal{S}\) be the solid obtained by rotating \(\mathcal{R}\) about \(L\text{.}\)

Compute \(\operatorname{vol} \mathcal{S}\text{.}\)
Sketch the solid \(\mathcal{S}\text{.}\) How else could we have computed the volume in (a)?

Solution.

As the diagram below indicates, when rotating the given region about the line \(y=2\text{,}\) we get cross sections \(\mathcal{S}_x\) that are discs of radius \(r_x=f(x)-2\text{.}\) Using the disc formula, we conclude that

\begin{align*} \operatorname{vol}\mathcal{S} \amp =\int_0^7\pi(f(x)-2)^2\, dx\\ \amp =\int_0^7\pi(3-\frac{3}{7}x)^2\, dx\\ \amp = \pi \int_3^0-\frac{7}{3}u^2\, du \amp (u=3-\frac{3}{7}x, du=-\frac{3}{7}dx\\ \amp = 21 \pi\text{.} \end{align*}

Alternatively, we observe that the solid of revolution in this case is just a cone of radius \(3\) and height 7. From Example 1.9.4 we conclude that \(\operatorname{vol}\mathcal{S}=\frac{1}{3}\pi\cdot 3^3\cdot 7=21\pi\text{.}\)

Example 1.9.8. Washer example.

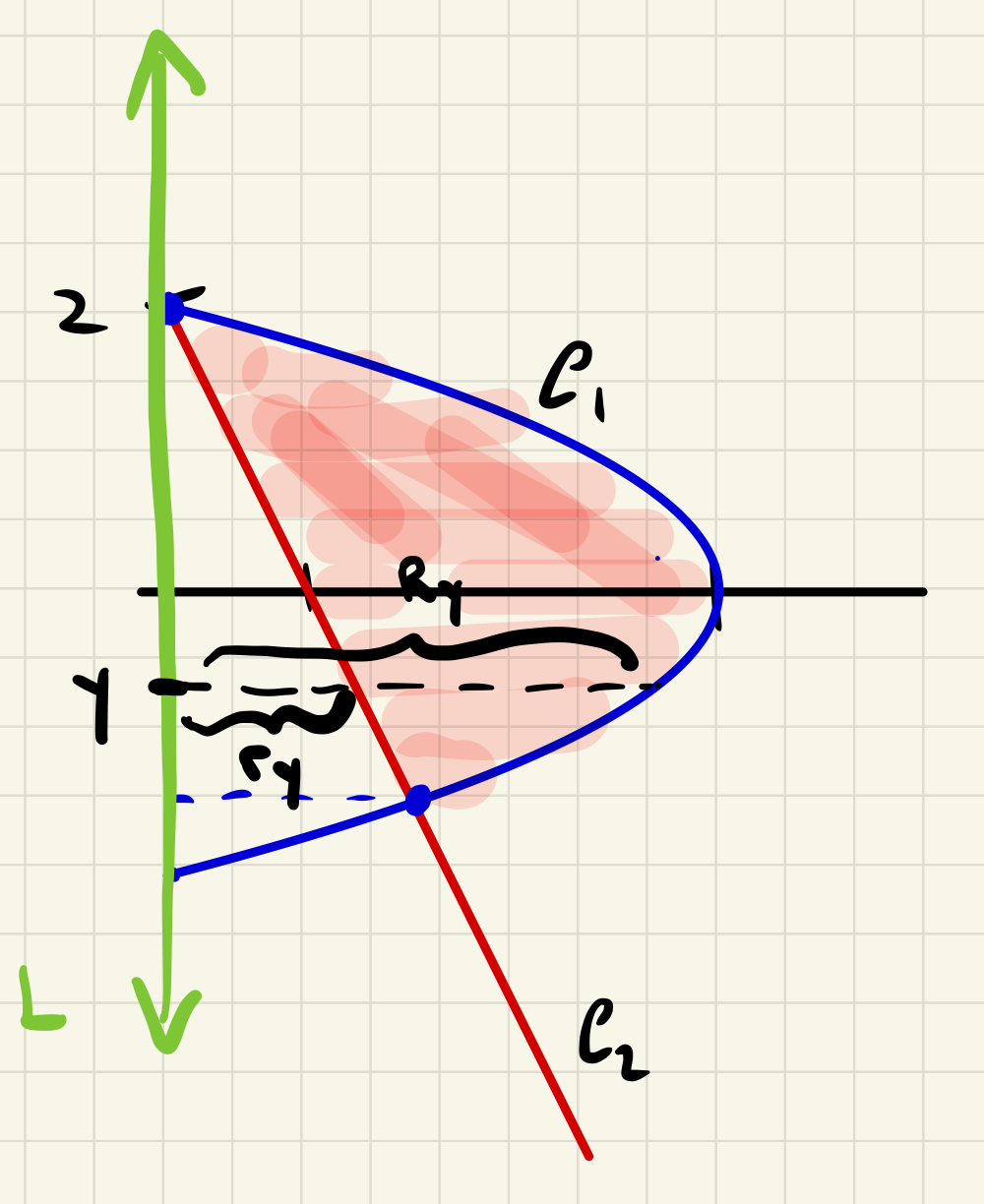
Let \(\mathcal{R}\) be the region enclosed by the line \(y+2x=2\) and the parabola \(y^2+x=4\text{,}\) and let \(\mathcal{S}\) be the solid obtained revolving \(\mathcal{R}\) about the \(y\)-axis. Sketch \(\mathcal{R}\) and compute the volume of \(\mathcal{S}\text{.}\)

Solution.

The two curves have equations \(x=p(y)=4-y^2\) and \(x=q(y)=1-y/2\text{.}\) We find the points of intersection of these two curves by solving the corresponding system of two equations for \(x\) and \(y\text{.}\) Setting \(x=4-y^2=1-y/2\text{,}\) we see that \(2y^2-y-6=0\text{.}\) Solving this quadratic yields \(y=2\) or \(y=-3/2\text{.}\) The two points of intersection are thus \((0,2)\) and \((7/4,-3/2)\text{.}\) It follows that the region \(\mathcal{R}\) is the set of points lying between the curves \(x=p(y)\) and \(x=q(y)\text{,}\) and the horizontal lines \(y=-3/2\) and \(y=2\text{.}\)

As indicated in the diagram below, the general \(y\)-cross section of this solid will be a washer of outer radius \(R_y=p(y)-0=p(y)\) and inner radius \(r_y=q(y)-0=q(y)\text{.}\) (The \(c\) in (1.9.5) is equal to 0 in this example.) We conclude that

\begin{align*} \operatorname{vol}\mathcal{S} \amp =\int_{-3/2}^2\pi(p(y)^2-q(y)^2)\, dy\\ \amp = \pi\int_{-3/2}^2(4-y^2)^2-(1-y/2)^2\, dy\\ \amp = \frac{2401\pi}{80}\text{,} \end{align*}

after some elementary, if tedious integration.

Prev Top Next