Skip to main content

Section 2.2 Line integrals of vector fields

Subsection 2.2.1 Vector fields

Definition 2.2.1. Vector fields.

A vector field is a function

\begin{align*} \boldF\colon \R^n \amp \rightarrow \R^n\\ (x_1,x_2,\dots, x_n)\amp\mapsto \left\langle F_1\langle x_1,x_2,\dots, x_n),F_2(x_1,x_2,\dots, x_n),\dots ,F_n(x_1,x_2,\dots, x_n)\right\rangle \text{.} \end{align*}

The scalar functions \(F_i\) are called the component functions. The vector field \(\boldF\) is continuous, differentiable, continuously differentiable, etc., if each of the component functions is continuous, differentiable, continuously differentiable, etc.

Subsection 2.2.2 Line integrals of vector fields

Definition 2.2.3. Integral of a vector field along a curve.

Let \(\boldr\colon \R\rightarrow \R^n\) be a smooth parametrization of the curve \(\mathcal{C}\subseteq\R^n\text{,}\) and let \(\boldT(t)=\boldr'(t)/\abs{\boldr'(t)}\) be the unit tangent vector of \(\boldr\text{.}\) Given a vector field \(\boldF\colon \R^n\rightarrow \R^n\) that is continuous on the curve \(\mathcal{C}\subseteq \R^n\text{,}\) we define its line integral, denoted \(\int_\mathcal{C}\boldF\cdot d\boldr\text{,}\) as

\begin{align} \int_\mathcal{C}\boldF\cdot d\boldr\amp=\int_\mathcal{C}\boldF\cdot\boldT\, ds\tag{2.2.1}\\ \amp =\int_a^b\boldF(\boldr(t))\cdot\frac{\boldr'(t)}{\abs{\boldr'(t)}}\, \abs{\boldr'(t)}\, dt \tag{2.2.2}\\ \amp = \int_a^b\boldF(\boldr(t))\cdot \boldr'(t)\, dt\text{.}\tag{2.2.3} \end{align}

Remark 2.2.4. Vector field line integral notation.

The first equality among (2.2.1)–(2.2.3) should be considered purely notational: i.e., it states simply that the integral being defined can be denoted by either of the expressions \(\int_C \boldF\cdot d\boldr\) or \(\int_\mathcal{C}\boldF\cdot \boldT\, ds\text{.}\) The remaining equalities (2.2.2)–(2.2.3) then give actual meaning to these two expressions.

Example 2.2.5. Vector line integral in plane.

Let \(\boldF(x,y)=(xy,x+y)\text{.}\)

  1. Compute the integral of \(\boldF\) along the segment \(\mathcal{C}\) of the curve \(x=y^2\) that starts at \((1,-1)\) and ends at \((4,2)\text{.}\)

  2. Compute the integral of \(\boldF\) along the reverse \(-\mathcal{C}\) of the path in (1): i.e., the segment of the curve \(x=y^2\) that starts at \((4,2)\) and ends at \((1,-1)\text{.}\)

Solution.

  1. We parametrize \(\mathcal{C}\) as \(\boldr(t)=(t^2,t)\text{,}\) \(-1\leq t\leq 2\text{.}\) Now compute

    \begin{align*} \int\limits_{\mathcal{C}}\boldF\cdot d\boldr \amp = \int_{-1}^2\boldF(t^2,t)\cdot \boldr'(t)\, dt \\ \amp = \int_{-1}^2\angvec{t^3,t^2+t}\cdot\angvec{2t,1}\, dt \\ \amp = \int_{-1}^22t^4+t^2+t\, dt\\ \amp =\left(\frac{2}{5}t^5+\frac{1}{3}t^3+\frac{1}{2}t^2\right)\Bigr\vert_{-1}^2\\ \amp = \frac{177}{10}\text{.} \end{align*}

  2. According to Remark 2.2.6 we should have \(\int_{-\mathcal{C}}\boldF\cdot d\boldr=-\int_{\mathcal{C}}\boldF\cdot d\boldr\text{.}\) We verify this directly by parametrizing \(-\mathcal{C}\) and computing. In general if \(\mathcal{C}\) is parametrized by \(\boldr(t)\text{,}\) where \(a\leq t\leq b\text{,}\) then \(-\mathcal{C}\) is parametrized by \(\bolds(t)=\boldr(-t)\text{,}\) where \(-b\leq t\leq -a\text{.}\) Indeed, since \(\bolds(t)=\boldr(-t)\text{,}\) we have \(\bolds(-b)=\boldr(b)\) and \(\bolds(-a)=\boldr(a)\text{.}\) Thus in our case we can parametrize \(-\mathcal{C}\) as \(\bolds(t)=((-t)^2,-t)=(t^2,-t)\text{,}\) where \(-2\leq t\leq 1\text{.}\) Now compute

    \begin{align*} \int_{-\mathcal{C}}\boldF\cdot d\boldr \amp = \int_{-2}^1\boldF(\bolds(t))\cdot \bolds'(t)\, dt\\ \amp = \int_{-2}^1\boldF(t^2,-t)\cdot \angvec{2t,-1}\, dt \\ \amp =\int_{-2}^1\angvec{-t^3,t^2-t}\cdot \angvec{2t,-1}\, dt\\ \amp =\int_{-2}^1-2t^4-t^2+t\, dt\\ \amp =-\frac{177}{10}\text{.} \end{align*}

Remark 2.2.6. Independence of parametrization.

Let \(\boldr\) and \(\bolds\) be two smooth parametrizations of the curve \(\mathcal{C}\) between the points \(P\) and \(Q\text{.}\)

  1. Denote by \(\mathcal{C}_1\) the curve \(\mathcal{C}\) with parametrization \(\boldr\text{,}\) and \(\mathcal{C}_2\) the curve \(\mathcal{C}\) with parametrization \(\bolds\text{.}\) If \(\boldr, \bolds\) both traverse \(\mathcal{C}\) exactly once, and in the same direction (e.g., both start at \(P\) and end at \(Q\)), then

    \begin{equation*} \int_{\mathcal{C}_1}\boldF\cdot d\boldr=\int_{\mathcal{C}_2}\boldF\cdot d\boldr \end{equation*}

    for any continuous vector field \(\boldF\text{.}\)

  2. If \(\boldr, \bolds\) both traverse \(\mathcal{C}\) exactly once, but \(\bolds\) starts where \(\boldr\) ends, and vice-versa, then we call the parametrization \(\bolds\) a reverse of \(\boldr\text{.}\) Denote by \(\mathcal{C}\) the curve as parametrized by \(\boldr\text{,}\) and \(-\mathcal{C}\) the curve as parametrized by the reverse path \(\bolds\text{.}\) We have

    \begin{equation*} \int_{-\mathcal{C}}\boldF\cdot d\boldr=-\int_\mathcal{C}\boldF\cdot d\boldr\text{.} \end{equation*}

Example 2.2.7. Vector field integral over helix.

Let \(\mathcal{C}\) be the helix with parametrization \(\boldr(t)=(\cos t, \sin t, t)\text{,}\) \(0\leq t\leq 2\pi\text{.}\) Compute \(\int_\mathcal{C}\boldF\cdot d\boldr\text{,}\) where \(\boldF=\angvec{-y,z,2x}\text{.}\)

Solution.

We have

\begin{align*} \int_\mathcal{C}\boldF\cdot d\boldr \amp = \int_0^{2\pi}\boldF(\boldr(t))\cdot \boldr'(t)\, dt\\ \amp =\int_0^{2\pi}\boldF(\cos t, \sin t, t)\cdot \angvec{-\sin t, \cos t, 1}\, dt \\ \amp =\int_0^{2\pi}\angvec{-\sin t, t,2\cos t}\cdot \angvec{-\sin t, \cos t, 1}\, dt\\ \amp =\int_0^{2\pi}\sin^2 t+t\cos t+2\cos t\, dt\\ \amp = \pi\text{.} \end{align*}

(To perform the integration in the penulitimate line, use the double-angle formula \(\sin^2 t=\frac{1}{2}(1-\cos 2\t)\text{,}\) and integration by parts.)

Definition 2.2.8. Line integrals with respect to \(dx, dy, dz\).

Let \(\boldr(t)=(g_1(t),g_2(t),g_3(t))\text{,}\) \(a\leq t\leq b\text{,}\) be a smooth parametrization of the curve \(\mathcal{C}\subseteq\R^n\text{.}\) Given a vector field \(\boldF=(F_1, F_2,F_3)\) that is continuous on the curve \(\mathcal{C}\subseteq \R^n\text{,}\) we define the line integrals with respect to \(dx, dy, dz\) as follows.

\begin{align*} \int_\mathcal{C}F_1\, dx \amp :=\int_a^b F_1(\boldr(t))\, g_1'(t)\, dt \\ \int_\mathcal{C}F_2\, dy \amp :=\int_a^b F_2(\boldr(t))\, g_2'(t)\, dt \\ \int_\mathcal{C}F_3\, dz \amp :=\int_a^b F_3(\boldr(t))\, g_3'(t)\, dt \text{.} \end{align*}

From Definition 2.2.3 we see that we have

\begin{align*} \int_\mathcal{C}\boldF\cdot d\boldr\amp =\int_\mathcal{C}F_1\, dx +\int_\mathcal{C}F_2\, dy +\int_\mathcal{C}F_3\, dz\\ \amp = \int_{\mathcal{C}}F_1\, dx+F_2\, dy+F_3\, dz \amp \text{(abbreviated notation)}\text{.} \end{align*}

To make sense of what a vector field line integral computes in a given context, it is best to consider its formulation as the scalar line integral of the scalar function \(\boldF\cdot \boldT\text{.}\) Given a partition of a parametrized curve into curve segments with endpoints

\begin{equation*} P=\boldr(a), P_1=\boldr(t_1),\dots, P_{n-1}=\boldr(t_{n-1}), P_n=\boldr(t_n) \end{equation*}

we have

\begin{equation*} \int_\mathcal{C}\boldF\cdot T\, ds\approx \sum_{k=1}^n \boldF(x_k, y_k, z_k)\cdot \boldT(x_k, y_k, z_k)\Delta s_k, \end{equation*}

where \((x_k,y_k,z_k)\) is a sample point in the \(k\)-th segment of the partition of \(\mathcal{C}\text{,}\) and \(\Delta s_k\) is the arc length of that segment. Focusing in on one term \(\boldF(x_k, y_k, z_k)\cdot \boldT(x_k, y_k, z_k)\Delta s_k\) and recalling our dot product cosine formula

\begin{equation*} \boldF\cdot \boldT=\abs{\boldF}\abs{\boldT}\cos\theta\text{,} \end{equation*}

where \(\theta\) is the angle between \(\boldF\) and \(\boldT\) at \((x_k, y_k, z_k)\text{,}\) we see that this term multiplies the component of \(\boldF\) in the direction of \(\boldT\) by the arc length \(\Delta s_k\) of the \(k\)-th segment. We have thus reduced our interpretation problem to understanding what type of quantity is obtained by summing these products. The definition of work and circulation below are two examples of doing just this.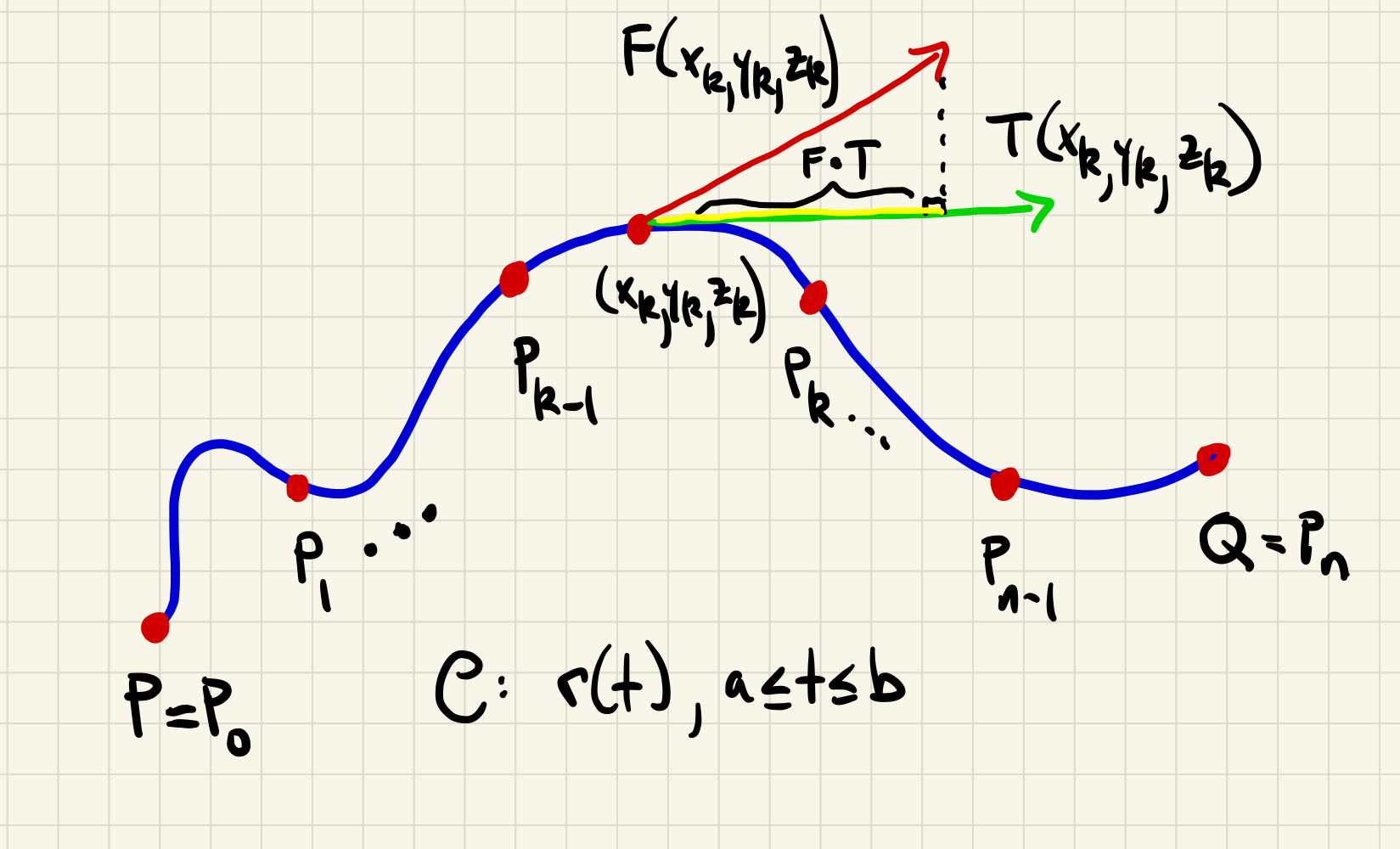

Figure 2.2.9. Interpreting \(\int_\mathcal{C}\boldF\cdot \boldT\, ds\)

Definition 2.2.10. Work and flow.

Let \(\boldr\colon [a,b]\rightarrow \R^m\) be a a smooth parametrization of the curve \(\mathcal{C}\subseteq\R^n\text{,}\) and assume the vector field \(\boldF\colon \R^n\rightarrow \R^n\) is continuous on \(\mathcal{C}\text{.}\)

  1. If \(\boldF(x_1,x_2,\dots, x_n)\) is the force acting at the point \((x_1,x_2,\dots, x_n)\text{,}\) then \(\int_\mathcal{C}\boldF\cdot d\boldr\) is the work \(W\) done in moving an object along the path \(\boldr\) from \(P=\boldr(a)\) to \(Q=\boldr(b)\text{.}\) You can show that \(W\) is equal to the change of kinetic energy the object undergoes as it moves from \(P\) to \(Q\text{.}\)

  2. If \(\boldF(x_1,x_2,\dots, x_n)\) is the velocity vector of a fluid at the point \((x_1,x_2,\dots, x_n)\text{,}\) then \(\int_\mathcal{C}\boldF\cdot d\boldr\) is the flow along the path \(\boldr\) from \(\boldr(a)\) to \(\boldr(b)\text{.}\) The path \(\boldr\) is simple (one-to-one except possibly at the endpoints) and closed (\(\boldr(a)=\boldr(b)\)), then the line integral is called the circulation around \(\mathcal{C}\text{.}\) We write \(\oint_\mathcal{C}\boldF\cdot d\boldr\) in this case to indicate the \(\mathcal{C}\) is closed.

Example 2.2.11. Circulation.

Let \(\mathcal{C}\) be the unit circle \(x^2+y^2=1\text{,}\) oriented in the counterclockwise direction. Compute the the circulation around \(\mathcal{C}\) for the given fluid velocity field.

  1. \(\displaystyle \boldF(x,y)=\angvec{x-y,x+y}\)

  2. \(\displaystyle \boldF(x,y)=\angvec{x,y}\)

Solution.

  1. Parametrize \(\mathcal{C}\) as \(\boldr( t )=(\cos t ,\sin t )\text{,}\) \(0\leq t \leq 2\pi\text{.}\) Now compute

    \begin{align*} \int\limits_\mathcal{C}\boldF\cdot d\boldr \amp =\int_0^{2\pi}\boldF(\cos t , \sin t )\cdot\boldr'(t)\, d t \\ \amp =\int_0^{2\pi}\angvec{\cos t -\sin t ,\cos t +\sin t }\cdot \angvec{-\sin t ,\cos t }\, d t \\ \amp=\int_0^{2\pi}-\cos t \sin t +\sin^2 t +\cos^2 t +\cos t \sin t \, d t \\ \amp =\int_0^{2\pi}1 d t \\ \amp =0 \end{align*}

  2. For any point on the circle, its tangent vector points orthogonally to its position vector. It follows that in this case \(\boldF(x,y)=\angvec{x,y}\) is always orthogonal to the tangent vectors on the curve (equivalently, that the tangential component of \(\boldF\) is always zero), and hence that the line integral is 0. More explicitly, using the parametrization \(\boldr(t)=(\cos t, \sin t)\) we have

    \begin{align*} \boldF(\boldr(t))\cdot \boldr'(t) \amp =\angvec{\cos t, \sin t}\cdot \angvec{-\sin t, \cos t}\\ \amp=-\cos t\sin t+\cos t\sin t=0 \text{.} \end{align*}

It is not difficult to modify our Sage cell from Sage example 2.1.2 to compute vector line integrals. As in that example, we use the vector() function to make vector objects out of our lists: this is essential for using vector operations like dot product, norm, etc.. Here is the line integral from Example 2.2.7.

Subsection 2.2.3 Flux across a planar curve

Definition 2.2.12. Flux.

The flux of a continuous vector field \(F\colon \R^2\rightarrow \R^2\) across a smooth simple closed curve \(\mathcal{C}\subseteq \R^2\) is defined as

\begin{equation*} \int_\mathcal{C}\boldF\cdot \boldn \, ds\text{,} \end{equation*}

where \(\boldn\) is the outward unit normal vector to \(\mathcal{C}\text{.}\)

If \(\boldr(t)=(g_1(t),g_2(t))\) is a parametrization of \(\mathcal{C}\) with counterclockwise (positive) orientation, then the outward unit normal vector can be expressed as

\begin{equation*} \boldn(t)=\frac{\angvec{g_2'(t),-g_1'(t)}}{\sqrt{g_1^2(t)+g_2^2(t)}}\text{.} \end{equation*}

Furthermore, if \(\boldF(x,y)=\angvec{F_1(x,y),F_2(x,y)}\text{,}\) then

\begin{align*} \oint_\mathcal{C}\boldF\cdot \boldn \, ds\amp = \int_a^b\angvec{F_1(\boldr(t)),F_2(\boldr(t))}\cdot \angvec{g_2'(t),-g_1'(t)}\, dt\\ \amp = \int_a^b F_1(g_1(t),g_2(t))g_2'(t)-F(g_1(t),g_2(t))g_1'(t)\, dt\\ \amp = \oint_\mathcal{C} F_1\, dy -F_2\, dx\text{.} \end{align*}

Example 2.2.13. Flux.

Let \(\mathcal{C}\) be the unit circle \(x^2+y^2=1\text{,}\) oriented in the counterclockwise direction. Compute the the flux around \(\mathcal{C}\) for the given fluid velocity field.

  1. \(\displaystyle \boldF(x,y)=\angvec{x-y,x+y}\)

  2. \(\displaystyle \boldF(x,y)=\angvec{x,y}\)

Solution.

Parametrize \(\mathcal{C}\) as \(\boldr(t)=(\cos t, \sin t)\text{,}\) \(0\leq t\leq 2\pi\text{.}\) It follows that \(\boldr'(t)=\angvec{-\sin t, \cos t}\text{,}\) and hence that the outward unit normal vector is \(\boldn(t)=\angvec{\cos t, \sin t}\text{.}\) We now compute the flux in each case using Definition 2.2.12.

  1. \begin{align*} \int_\mathcal{C}\boldF\cdot \boldn\, ds \amp= \int_0^{2\pi}\boldF(\cos t, \sin t)\cdot \boldn(t)\, ds \\ \amp = \int_0^{2\pi}\angvec{\cos t-\sin t, \cos t+\sin t}\cdot \angvec{\cos t, \sin t}\, dt\\ \amp = \int_0^{2\pi} \cos^2 t-\cos t\sin t+\cos t\sin t+\sin^2 t\, dt\\ \amp = \int_0^{2\pi}1\, dt\\ \amp = 2\pi\text{.} \end{align*}

  2. \begin{align*} \int_\mathcal{C}\boldF\cdot \boldn\, ds \amp= \int_0^{2\pi}\boldF(\cos t, \sin t)\cdot \boldn(t)\, ds \\ \amp = \int_0^{2\pi}\angvec{\cos t, \sin t}\cdot \angvec{\cos t, \sin t}\, dt\\ \amp = \int_0^{2\pi} 1 dt\\ \amp = 2\pi\text{.} \end{align*}