Appendix D Examples
0.1 Sets and functions
Example 0.1.15 Arithmetic operations as functions
Example 0.1.20 Role of domain and codomain in injectivity and surjectivity
0.2 Logic
Example 0.2.7 Modeling “Every positive number has a square-root”
Example 0.2.10 The limit does not exist
1.1 Double integrals over rectangles
Example 1.1.4 Nonintegrable functions
Example 1.1.8 Volume below graph
1.2 Iterated integrals and Fubini's theorem
Example 1.2.5 Volume below graph revisited
Example 1.2.6 Fubini examples
1.3 Double integrals over general regions
Example 1.3.8 Fubini's theorem over elementary planar regions
Example 1.3.10 Using double integral properties
1.4 Area of planar regions and average value
Example 1.4.3 Area of planar regions
Example 1.4.5 Average temperature over region
1.5 Triple integrals
Example 1.5.11 Triple integral over a box
Example 1.5.12 Volume of tetrahedron
Example 1.5.13 Volume of slice of parabolic cylinder
Example 1.5.14 Region from iterated integral
1.6 Substitution: general
Example 1.6.9 Substitution: linear, two variables
Example 1.6.10 Volume of ellipsoid
1.7 Substitution: polar and cylindrical coordinates
Example 1.7.5 Area between limaçon and circle
Example 1.7.6 Average value over semicircle
Example 1.7.11 Volume of sphere: cylindrical coordinates
Example 1.7.12 Average value over hemisphere: cylindrical coordinates
1.8 Substitution: spherical coordinates
Example 1.8.5 Average distance over a solid sphere
Example 1.8.6 Volume of ice cream cone
1.9 Applications of multiple integrals
Example 1.9.2 Centroids of triangles
Example 1.9.3 Centroid of hemisphere
Example 1.9.6 Joint probability density function
Example 1.9.9 Joint probability density function
2.1 Line integrals of scalar functions
Example 2.1.11 Line integral of helix
Example 2.1.12 Area of a curtain
Example 2.1.13 Mass of wire
2.2 Line integrals of vector fields
Example 2.2.5 Vector line integral in plane
Example 2.2.7 Vector field integral over helix
Example 2.2.11 Circulation
Example 2.2.13 Flux
2.3 Path independence, conservative fields, potential functions
Example 2.3.2 Gradient vector fields
Example 2.3.5 A non-gradient vector field
Example 2.3.6 Work done by gravity
Example 2.3.15 Curl test: conclusive
Example 2.3.16 Curl test: inconclusive
Example 2.3.20 Curl test: complete
2.4 Green's theorem in the plane
Example 2.4.2 Circulation around semicircle
Example 2.4.5 Area of astroid
Example 2.4.10 Flux across square
Example 2.4.13 Visualizing curl and divergence
2.5 Surfaces and their area
Example 2.5.3 Plane parametrization
Example 2.5.5 Sphere of radius \(R\) parametrization
Example 2.5.6 Circular cylinder
Example 2.5.7 Parametrizing graphs of functions
Example 2.5.8 Cone parametrization
Example 2.5.12 Tangent plane
Example 2.5.14 Surface area of sphere
Example 2.5.15 Surface area of paraboloid
2.6 Surface integrals
Example 2.6.8 Piecewise smooth surface
Example 2.6.10 Orientations of the sphere
Example 2.6.11 Graph of function
Example 2.6.14 Flux across a sphere
Example 2.6.16 Flux across a cone
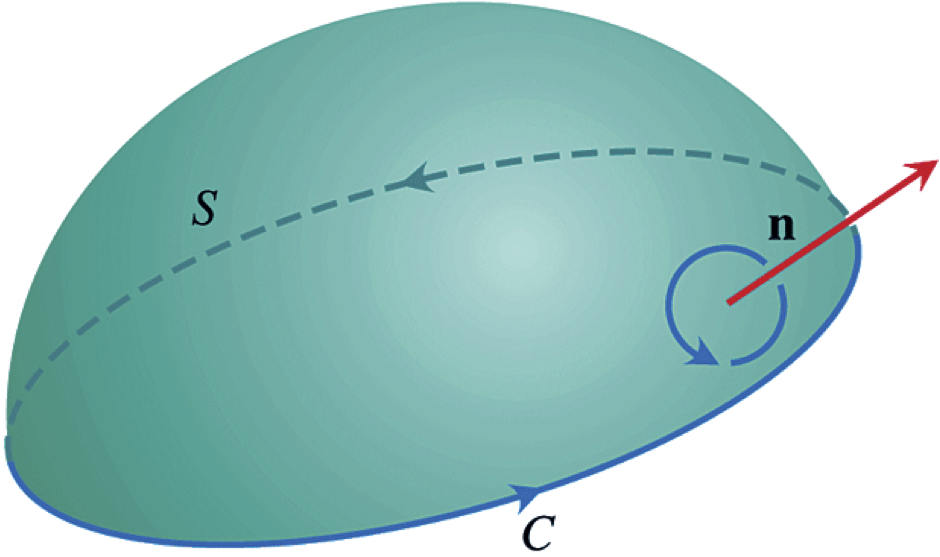
2.7 Stokes's theorem
Example 2.7.4 Line integral over triangle
Example 2.7.5 Stokes for a pringle
Example 2.7.7 Stokes for sliced cylinder
Example 2.7.8 Stokes's implies Green's
2.8 Divergence theorem
Example 2.8.3 Flux out of cube
Example 2.8.9 Gauss's law