Section 2.7 Stokes's theorem
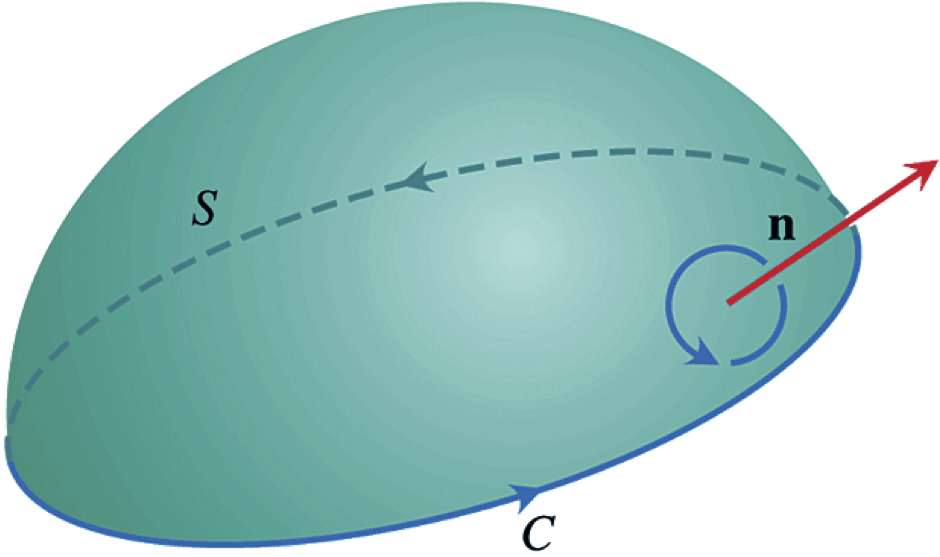
Definition 2.7.1. Induced orientation.
Let \(\mathcal{S}\) be a smooth surface with orientation \(\boldn\colon \mathcal{S}\rightarrow \R^3\text{.}\) Given a simple curve \(\mathcal{C}\subseteq \mathcal{S}\) lying partly on the boundary of \(\mathcal{S}\) the induced orientation on \(\mathcal{C}\) is the one given by the following right-hand rule: if your thumb points along \(\boldn\text{,}\) then your fingers curl in the direction of the orientation of \(\mathcal{C}\text{.}\) Alternatively, the orientation of \(\mathcal{C}\) is induced by \(\boldn\) if looking down along \(\boldn\text{,}\) the orientation of \(\mathcal{C}\) is such that the portion of \(\mathcal{S}\) the curve bounds lies on the left.
Definition 2.7.2. Orientation of piecewise smooth surface.
Let \(\mathcal{S}=\cup_{i=1}^k\mathcal{S}_k\) be a piecewise smooth surface, and assume each surface \(\mathcal{S}_k\) is orientable. An orientation of \(\mathcal{S}\) is a choice of orientations \(\boldn_k\) on each surface \(\mathcal{S}_k\) such that the following condition is satisfied: given any two surfaces \(\mathcal{S}_{k_1}, \mathcal{S}_{k_2}\) intersecting in the curve \(\mathcal{C}\text{,}\) the orientation induced on \(\mathcal{C}\) by the orientation \(\boldn_{k_1}\) is the opposite of the orientation induced by the orientation \(\boldn_{k_2}\text{.}\)
Theorem 2.7.3. Stokes's theorem.
Let \(\mathcal{S}\) be a piecewise smooth oriented surface whose boundary \(\partial \mathcal{S}=\mathcal{C}\) is a union of closed, piecewise smooth, simple curves. If \(\boldF\) is a continuous vector field whose component functions have continuous first-order partial derivatives on an open set containing \(\mathcal{S}\text{,}\) then
where (a) \(\boldn\) is the orientation of \(\mathcal{S}\) and (b) the line integral is computed with respect to the induced orientation on \(\mathcal{C}\text{.}\)
Example 2.7.4. Line integral over triangle.
Let \(\mathcal{C}\) be the triangle with vertices \((1,0,0), (0,1,0), (0,0,1)\) oriented counterclockwise from above. Compute \(\oint_\mathcal{C}\boldF\cdot \boldr\text{,}\) where \(\boldF(x,y,z)=\angvec{z^2, y^2, x}\text{.}\)
-
Identify as boundary of surface.
We have \(\mathcal{C}=\partial \mathcal{S}\text{,}\) where \(\mathcal{S}\) is the triangular region enclosed by \(\mathcal{C}\text{.}\)
-
Parametrize surface.
The region \(\mathcal{S}\) is the region of the plane \(x+y+z=1\) lying above the triangular region \(\mathcal{R}\colon 0\leq x\leq 1, 0\leq y\leq 1-x\text{.}\) Writing \(z=1-x-y\text{,}\) we have parametrization
\begin{align*} \boldr(x,y) \amp=(x,y,1-x-y) \\ \mathcal{R}\colon 0\amp\leq x\leq 1, 0\leq y\leq 1-x \text{.} \end{align*} -
Identify appropriate orientation of surface.
For the induced orientation on \(\mathcal{C}\) to be counterclockwise from above, we want the upward orientation on \(\mathcal{S}\text{.}\) We know that for a parametrization of the form \(r(x,y)=(x,y,1-x-y)\) the orientation
\begin{equation*} \boldn(x,y,z)=\frac{\boldr_x\times \boldr_y}{\abs{\boldr_x\times \boldr_y}} \end{equation*}is the upward one. For the step below we need just the denominator of this expression: \(\boldr_x\times \boldr_y=\angvec{1,1,1}\text{.}\)
-
Integrate \(\curl\boldF\).
A straightforward computation gives us \(\curl\boldF=\angvec{0,2z-1,0}\text{.}\) Using Theorem 2.6.15 we have
\begin{align*} \iint_\mathcal{S}\curl\boldF\cdot \boldn\, d\sigma \amp= \iint_{\mathcal{R}}\curl\boldF(\boldr(x,y))\cdot (\boldr_x\times \boldr_y)\, dA \\ \amp=\int_0^1\int_0^{1-x}\angvec{0,2(1-x-y)-1,0}\cdot\angvec{1,1,1}\, dy\, dx \\ \amp = \int_0^1\int_0^{1-x}1-2(x+y)\, dy\, dx\\ \amp \int_0^1 \left(y-(x+y)^2\Bigr_0^{1-x}\, dx\\ \amp =\int_0^1 x^2-x\, dx\\ \amp = \frac{1}{3}-\frac{1}{2}=-\frac{1}{6} \end{align*}
Example 2.7.5. Stokes for a pringle.
Let \(\mathcal{S}\) be a portion of the surface \(z=y^2-x^2\) lying within the cylinder \(x^2+y^2=1\text{,}\) and let \(\mathcal{C}\) be its boundary. Let \(\boldn\colon \mathcal{S}\rightarrow \R^3\) be the upward orientation on \(\mathcal{S}\text{.}\) Verify Stokes's theorem for \(\mathcal{S}, \mathcal{C}\text{,}\) and the vector field \(\boldF=y\boldi-x\boldj+x^2\boldk\text{.}\)
I include this mainly as a nice parametrization example. The surface is parametrized using cylindrical coordinates as
and the boundary curve \(\mathcal{C}\) with counterclockwise orientation has parametrization
(Evaluate Sage cell below for a visualization.) Next compute
Since the \(z\)-component of \(\boldr_r\times\boldr_\theta\) is \(r\geq 0\text{,}\) we see that it gives rise to the given choice of upward orientation. With all the ingredients assembled, I leave it to you to verify that
Corollary 2.7.6. Two surfaces, same boundary.
Let \(\mathcal{S}_1, \mathcal{S}_2\) be two piecewise smooth oriented surfaces with a shared boundary curve \(\mathcal{C}\) satisfying the conditions of Stokes's theorem, and assume that the orientation on \(\mathcal{C}\) induced by \(\mathcal{S}_1\) is equal to the orientation induced by \(\mathcal{S}_2\text{.}\) If \(\boldF\) is a continuous vector field whose component functions have continuous partial derivatives on an open set containing \(S_1\) and \(S_2\text{,}\) then
where \(\boldn_1, \boldn_2\) are the orientations of \(\mathcal{S}_1,\mathcal{S}_2\text{,}\) respectively.
Example 2.7.7. Stokes for sliced cylinder.
Let \(\boldF=\angvec{-y^2, x, z^2}\text{,}\) and let \(\mathcal{C}\) be the intersection of the cylinder \(x^2+y^2=1\) and the plane \(y+z=2\text{.}\) Compute \(\oint_\mathcal{C}\boldF\cdot \boldr\text{,}\) where \(\mathcal{C}\) is oriented counterclockwise, viewed from above.
Solution 1.
The curve \(\mathcal{C}\) is the boundary of the elliptical region \(\mathcal{S}\) it encloses in the plane \(y+z=2\text{.}\) Since \(z=2-y\) for points on this plane, we can parametrize as
Assembling ingredients we have
Since the \(z\)-component of \(\boldr_r\times\boldr_\theta\) is nonnegative, we see that this gives rise to the upward orientation on \(\mathcal{S}\text{,}\) which induces the counterclockwise orientation on \(\mathcal{C}\text{.}\) We can now use Stokes's theorem to concude
Solution 2.
Alternatively, we can treat \(\mathcal{C}\) as the boundary of the piecewise smooth surface \(\mathcal{S}=\mathcal{S}_1\cup \mathcal{S}_2\text{,}\) where \(\mathcal{S}_1\) is the portion of the cylinder \(x^2+y^2=1\) above the \(xy\)-plane and below the plane \(y+z=2\text{,}\) and \(\mathcal{S}_2\) is the disc \(x^2+y^2\leq 1\) in the \(xy\)-plane. To have the given orientation of \(\mathcal{C}\) be induced by that of \(\mathcal{S}\text{,}\) we must choose the inward orientation \(\boldn\) on \(\mathcal{S}\) : this orientation is inward on the cylinder \(\mathcal{S}_1\) and upward on the disc \(\mathcal{S}_2\text{.}\) With this setup we have
A few comments are in order. We have \(\iint_{\mathcal{S}_1}\curl\boldF\cdot \boldn\, d\sigma=0\) because the normal vectors to the cylinder \(\mathcal{S}_1\) point horizontally, and thus are orthogonal to the curl vectors \(\curl\boldF\text{,}\) which point vertically. Secondly, on the disc in the \(xy\)-plane we clearly have the upward normal vector equal to \(\angvec{0,0,1}\text{.}\)
Example 2.7.8. Stokes's implies Green's.
Show that Stokes's theorem implies Green's theorem.
Let \(\mathcal{R}\) be the region enclosed by a simple, piecewise smooth planar curve \(\mathcal{C}\) oriented counterclockwise, and suppose \(\boldF(x,y)=\angvec{F_1(x,y),F_2(x,y)}\) satisfies the conditions of Theorem 2.4.1. Define \(G(x,y,z)=\angvec{F_1(x,y),F_2(x,y),0}\text{,}\) and think of \(\mathcal{R}\subseteq\R^3\) as a planar surface living in the \(xy\)-plane, with \(\mathcal{C}\) is boundary. We choose the orientation \(\boldn(x,y,z)=\angvec{0,0,1}=\boldk\) on \(\mathcal{R}\text{,}\) which induces the counterclockwise orientation on \(\mathcal{C}\text{.}\) By Stokes's theorem we have
Theorem 2.7.9. Curl interpretation.
Assume the component functions of \(\boldF=\angvec{F_1, F_2,F_3}\) have continuous first-order partial derivatives on an open set containing the point \(P=(x,y,z)\text{.}\) Let \(\boldn\) be any unit vector, and for all \(R > 0\text{,}\) let \(C_R\) be the circle of radius \(R\) centered at \(P\) and lying in the plane orthogonal to \(\boldn\text{.}\) We have
where the orientation of \(\mathcal{C}_R\) is chosen to be counterclockwise with respect to \(\boldn\text{.}\) As such, we interpret the quantity \(\curl\boldF\cdot \boldn(x,y,z)\) as the circulation density (in units circulation per unit area) of \(\boldF\) at \(P=(x,y,z)\) with respect to the axis of rotation \(\boldn\text{.}\)