Skip to main content

Functions and single-variable calculus A course resource for Math 218

Ellen Goldstein, Aaron Greicius

Section 1.7 Function composition

Subsection Learning Goals

  • Understand what it means to compose two functions
    🔗
    🔗
  • Calculate values of compositions of functions given tables, graphs, or formulas
    🔗
    🔗
  • Simplify the formula for a composition of functions
    🔗
    🔗
  • Determine the domain of a composition of functions
    🔗
    🔗
  • See an example where composition of functions is vital to studying calculus
    🔗
    🔗
🔗
🔗

Subsection Motivation and Examples

Recall that a function, by definition, is a process that takes a collection of inputs and produces a corresponding collection of outputs in such a way that the process produces one and only one output value for any single input value. Because every function is a process, it makes sense to think that it may be possible to take two function processes and do one of the processes first, and then apply the second process to the result.
🔗
Recall Dolbear’s function, \(F=f(N)=40+0.25N\text{,}\) from Example Example 1.3.8 that relates the number \(N\) of chirps per minute from a snowy cricket to the Fahrenheit temperature, \(F\text{.}\)
🔗
The Celsius and Fahrenheit temperature scales are connected by a linear function. Indeed, the function that converts Fahrenheit to Celsius is
\begin{equation*} C = g(F) = \frac{5}{9}(F-32) \end{equation*}
🔗
For instance, a Fahrenheit temperature of 32 degrees corresponds to \(C=g(32) = 0\) degrees Celsius.
🔗
If we are given a number of chirps, \(N\text{,}\) we can combine the two processes given by Dolbear’s function and the conversion from Fahrenheit to Celsius to obtain a new function \(C=h(N)\) that takes as input the number of chirps per minute and gives as output the temperature in degrees Celsius.
🔗

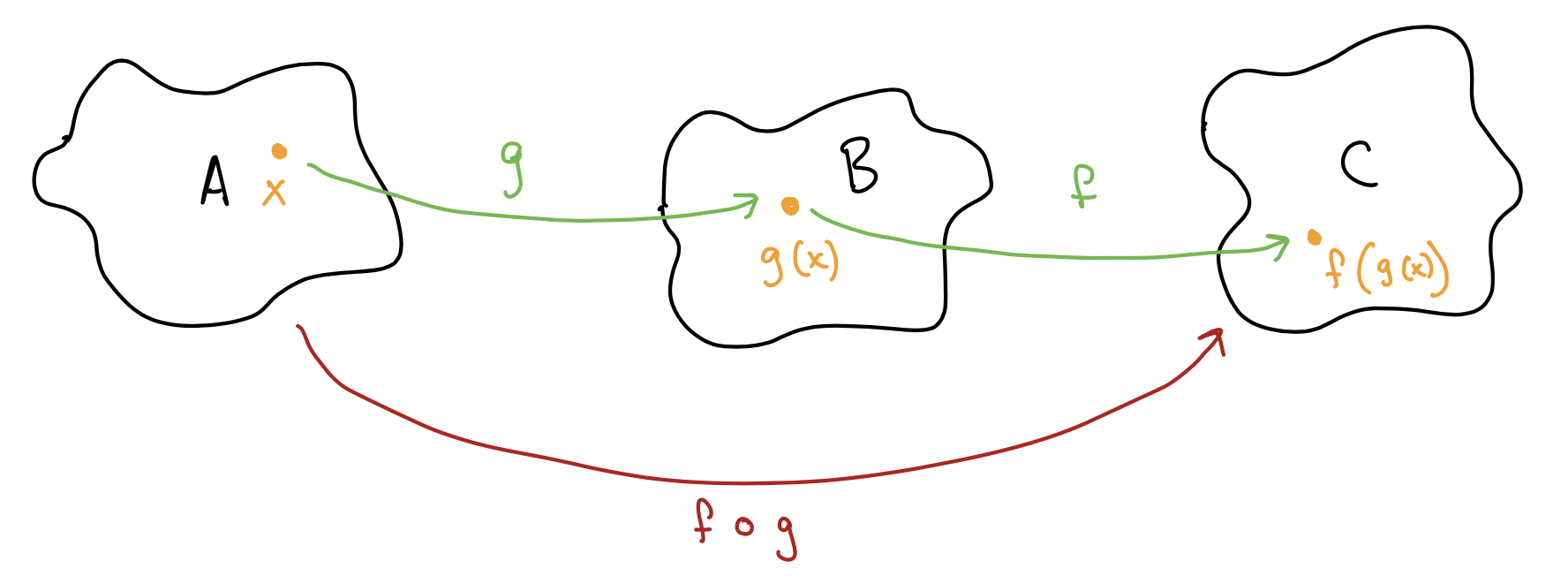
Example 1.7.1.

Using Dolbear’s model, what is the temperature in degrees Celsius assuming we observe crickets chirping at 80 chirps per minute?
🔗
Solution.
First, we compute that the temperature in degrees Fahrenheit is
\begin{equation*} F = D(80) = 40+0.25(80) = 60\text{.} \end{equation*}
🔗
It remains only to convert this Fahrenheit temperature to degrees Celsius:
\begin{equation*} C = G(60) = \frac{5}{9}(60-32) = \frac{140}{9} =15\frac{5}{9}^\circ C\text{.} \end{equation*}
Thus, if crickets chirp at 80 chirps per minute, Dolbear’s model predicts the temperature is \(9^\circ C\text{.}\)
🔗
🔗
🔗

Example 1.7.2.

Determine a formula for the new function \(C=h(N)\) that takes as input the number \(N\) of cricket chirps per minute and gives as output the temperature \(C\) in degrees Celsius.
🔗
Solution.
Using \(F=f(N)\) as the input for the function \(C=g(F)\text{,}\) we simplify to find a formula directly from \(N\) to \(C\) that does not involve the variable \(F\text{:}\)
\begin{equation*} \begin{aligned}C \amp = g(F)\\ \amp = g(f(N))\\ \amp = \frac{5}{9}(f(N)-32)\\ \amp = \frac{5}{9}((40+0.25N)-32)\\ \amp =\frac{5}{9}(8+0.25N) \end{aligned} \end{equation*}
🔗
So the function \(C=h(N)\) is given by
\begin{equation*} C = \frac{5}{9}(8+0.25N)\text{.} \end{equation*}
🔗
🔗
🔗
🔗

Subsection Function composition

The function \(h\) explored in the examples above is called the composition of \(f\) and \(g\text{,}\) denoted \(h=g\circ f\text{.}\) Let’s make this definition official.
🔗

Definition 1.7.3. Function composition.

Given a function \(f\colon B\rightarrow C\text{,}\) and a function \(g\) with domain \(A\) satisfying \(\range g\subseteq B\text{,}\) their composition \(f\circ g\) is the function \(f\circ g\colon A\rightarrow C\) defined as
\begin{equation} f\circ g\, (a)=f(g(a))\tag{1.52} \end{equation}
for all \(a\in A\text{.}\)
🔗
🔗
Figure 1.7.4. The composition \((f\circ g)(x) = f(g(x))\) uses the outputs \(g(x)\) of \(g\) as the inputs of \(f\text{.}\)
🔗

Remark 1.7.5. Function composition.

Observe the important condition in the setup of a composition of two functions \(f\) and \(g\text{:}\) we need the range of \(g\) to be a subset of the domain of \(f\text{.}\) Let’s think through why this must be the case.
🔗
By definition the composition function \(h=f\circ g\) takes an input \(x\) and maps it to the output
\begin{equation*} h(x)=f(g(x))\text{.} \end{equation*}
In order for this to make sense, we need \(g(x)\) to be in the domain of \(f\text{.}\) In other words, the outputs of \(g\) must lie in the domain of \(f\text{:}\) this is equivalent to saying that the range of \(g\) is a subset of the domain of \(f\text{.}\)
🔗
🔗

Warning 1.7.6. Composition is not multiplication.

The notation \(f\circ g\) for function composition is similar looking to the notation \(f\cdot g\) for function multiplication. Do not conflate these two operations! Indeed, comparing \(f\circ g\, (x)\) and \(f\cdot g\, (x)\) at an arbitrary input, we see that
\begin{align*} f\circ g\, (x) \amp =f(g(x))\\ f\cdot g\, (x) \amp =f(x)g(x)\text{,} \end{align*}
which are by no means the same thing.
🔗
🔗

Example 1.7.7. Composition: evaluation and formulas.

Let \(f(x)=1/x\) and \(g(x)=1/(x^2+1)\text{.}\) Define \(h=f\circ g\text{.}\)
  1. Compute \(h(-3)\text{.}\)
    🔗
    🔗
  2. Find a formula for \(h(x)\text{.}\)
    🔗
    🔗
🔗
Solution.
  1. By definition, we have
    \begin{align*} h(-3) \amp =f(g(-3))\\ \amp =f\left(\frac{1}{10}\right)\amp g(-3)=\frac{1}{(-3)^2+1}=\frac{1}{10}\\ \amp =\frac{1}{\frac{1}{10}}\\ \amp = 10\text{.} \end{align*}
    🔗
    🔗
  2. The formula for \(h\) is computed in much the same way as above, replacing \(-3\) with the variable \(x\text{:}\)
    \begin{align*} h(x) \amp =f(g(x))\\ \amp =f\left(\frac{1}{x^2+1}\right)\\ \amp =\frac{1}{\frac{1}{x^2+1}}\\ \amp =x^2+1\text{.} \end{align*}
    🔗
    🔗
  3. The implied domain of \(h\) is the set of \(x\in \R\) for which \(g\) is defined at \(x\) and \(f\) is defined at \(g(x)\text{.}\) The function \(g\) is defined at \(x\) as long as \(x^2+1\) is nonzero; but this is true for all \(x\text{,}\) since \(x^2+1\geq 1\) for all \(x\text{.}\) Similarly, the expression \(f(g(x))=1/g(x)\) is defined as long as \(g(x)\) is nonzero. As already observed, this is true for all \(x\text{.}\) Thus the implied domain of \(h\) is \(\R\text{.}\)
    🔗
    🔗
🔗
🔗
🔗

Example 1.7.8. Composition: order matters.

Define
\begin{align*} f\colon \R \amp \rightarrow \R \amp g\colon \R\amp \rightarrow \R \end{align*}
as \(f(x)=x^2+1\) and \(g(x)=-2x+1\text{.}\)
  1. Compute formulas for \(f\circ g\) and \(g\circ f\text{.}\)
    🔗
    🔗
  2. Do we have \(f\circ g=g\circ f\text{?}\)
    🔗
    🔗
🔗
Solution.
  1. We compute
    \begin{align*} f\circ g\, (x) \amp =f(g(x))\\ \amp = f(-2x+1)\\ \amp = (-2x+1)^2+1 \\ \amp = 4x^2-4x+2\\ g\circ f\, (x) \amp =g(f(x))\\ \amp = g(x^2+1)\\ \amp = -2(x^2+1)+1 \\ \amp = -2x^2-1\text{.} \end{align*}
    🔗
    🔗
  2. From the above we see that \(f\circ g\) and \(g\circ f\) are both quadratic polynomials. Recall that two polynomials of the same degree are equal as functions if and only if their coefficients are all equal. (See Corollary 1.5.26.) Comparing coefficients above, we see easily that \(f\circ g\ne g\circ f\text{.}\)
    🔗
    Moral of the story: the order of composition matters! That is, the function \(f\circ g\) is not necessarily the same as \(g\circ f\text{.}\)
    🔗
    🔗
🔗
🔗
🔗

Remark 1.7.9. Inner/outer function.

The function \(g\) in a composition \(h=f\circ g\) is often called the “inner function” of the composition, and \(f\) is called the “outer function”. This terminology derives naturally from the definition
\begin{equation} h(x)=\overset{\text{outer}}{\overbrace{f(\underset{\text{inner}}{\underbrace{g(x)}})}}\text{.}\tag{1.53} \end{equation}
Alternatively, we can use sequential language when describing the roles of \(f\) and \(g\) in the composition \(f\circ g\text{.}\) That is, when computing \(h(x)\) using definition (1.53), we first evaluate \(g\) at \(x\) to produce the output \(g(x)\text{,}\) and then evaluate \(f\) at \(g(x)\) to produce the output \(f(g(x))\text{.}\)
🔗
This sequential way of looking at composition is especially helpful when trying to describe a given function \(h\) as a composition \(h=f\circ g\) of two functions.
🔗
🔗

Example 1.7.10. Expressing functions as compositions.

Express the given function \(h\) as a composition \(h=f\circ g\text{.}\) Give explicit formulas for your choice of \(f\) and \(g\text{.}\)
  1. \(\displaystyle h(x)=\sqrt{x^2+x+1}\)
    🔗
    🔗
  2. \(\displaystyle h(x)=\frac{1}{3x-7}\)
    🔗
    🔗
🔗
Solution.
  1. The particular form of the of the formula here strongly suggests the the “outer function” \(f\) should be \(f(x)=\sqrt{x}\text{,}\) and the “inner function” \(g\) should be \(g(x)=x^2+x+1\text{.}\) Let confirm that \(h=f\circ g\text{:}\) for all \(x\text{,}\) we have
    \begin{align*} f(g(x)) \amp =\sqrt{g(x)} \amp (f(x)=\sqrt{x})\\ \amp =\sqrt{x^2+x+1} \amp (g(x)=x^2+x+1)\\ \amp =h(x) \end{align*}
    for all \(x\in \R\text{.}\) This proves \(h=f\circ g\text{.}\)
    🔗
    🔗
  2. In this example the “inner function” and “outer function” is less obvious. Let’s use the sequential description of function composition to help us out. Looking at the formula for \(h\text{,}\) we see that to evaluate \(h\) at a given \(x\text{,}\) we must first compute \(3x-7\text{,}\) and then compute the reciprocal of this expression \(1/(3x-7)\text{.}\) Thus suggests that we should set \(g(x)=3x-7\) and \(f(x)=1/x\text{.}\) Let’s check that our choice of \(f\) and \(g\) work: we have
    \begin{align*} f(g(x)) \amp =f(3x-7) \amp (g(x)=3x-7)\\ \amp =\frac{1}{3x-7} \amo (f(x)=1/x)\\ \amp =h(x) \end{align*}
    for all \(x\) in the implied domain of \(h\text{.}\) Thus \(h=f\circ g\text{.}\)
    🔗
    🔗
🔗
🔗
🔗
The next two examples illustrate how to compute values of a composition of functions when the function information is provided by tables or graphs.
🔗

Example 1.7.11. Composition: using tables.

Suppose that \(f\) and \(g\) are given by the table
🔗
  1. Compute the given expression or else explain why the tables do not provide enough information.
    1. \(\displaystyle f\circ g\, (2)\)
      🔗
      🔗
    2. \(\displaystyle g\circ f\, (2)\)
      🔗
      🔗
    3. \(\displaystyle g\circ f\, (0)\)
      🔗
      🔗
    🔗
    🔗
  2. Find all solutions to \(f\circ g\, (x)=6\) lying in the set \(\{0,1,2,3,4\}\text{.}\)
    🔗
    🔗
  3. Find all solutions to \(g\circ f\, (x)=2\) lying in the set \(\{0,1,2,3,4\}\text{.}\)
    🔗
    🔗
🔗
Solution.
  1. We compute
    \begin{align*} f\circ g\, (2) \amp =f(g(2))\\ \amp = f(0) \amp (g(2)=0)\\ \amp = 6 \end{align*}
    and
    \begin{align*} g\circ f\, (2) \amp = g(f(2))\\ \amp =g(3) \amp (f(2)=3)\\ \amp = 4\text{.} \end{align*}
    On the other hand, we do not have enough information from the table to compute \(g\circ f\, (6)\) since \(f(0)=6\) and the table does not indicate what \(g(6)\) is.
    🔗
    🔗
  2. First observe that \(f(x)=6\) for \(x=0,4\text{.}\) Thus for \(f(g(x))=6\) for \(x\in \{0,1,2,3,4\}\text{,}\) we need to find the \(x\) in this set such that \(g(x)=0\) or \(g(x)=4\text{.}\) From the table we see that \(g(2)=0\) and \(g(3)=4\text{.}\) Thus \(x=2,3\) are the two solutions to the equation \(f\circ g\, (x)=6\) lying in the set \(\{0,1,2,3,4\}\text{.}\)
    🔗
    🔗
  3. Our reasoning is similar to the previous part. Since \(g(x)=4\) for \(x=4\) and since the solutions to \(f(x)=4\) for \(x\in \{0,1,2,3,4\}\) are \(x=1\) and \(x=3\text{,}\) these are the solutions to \(g\circ f\, (x)=2\) lying in \(\{0,1,2,3,4\}\text{.}\)
    🔗
    🔗
🔗
🔗
🔗

Example 1.7.12. Composition: using graphs.

The graphs of functions \(p\) and \(q\) are given below.
🔗
Compute the following function values.
  1. \(p\circ q\, (0)\text{.}\)
    🔗
    🔗
  2. \(\displaystyle q\circ p\, (0)\)
    🔗
    🔗
  3. \(\displaystyle p\circ p \, (-3/2)\)
    🔗
    🔗
🔗
Solution.
  1. We have
    \begin{align*} p\circ q\, (0) \amp = p(q(0))\\ \amp = p(2)\\ \amp = 2\text{.} \end{align*}
    🔗
    🔗
  2. We have
    \begin{align*} q\circ p\, (0) \amp = q(p(0))\\ \amp = q(-1/2)\\ \amp = 2 \text{.} \end{align*}
    🔗
    🔗
  3. We have
    \begin{align*} p\circ p\, (-3/2) \amp = p(p(-3/2))\\ \amp = p(0)\\ \amp = -1/2\text{.} \end{align*}
    🔗
    🔗
🔗
🔗
🔗
🔗

Subsection Implied domain of compositions

How do we determine the implied domain of a composition \(f\circ g\) of two functions? For \(f(g(x))\) to be defined at \(x\text{,}\) we need two conditions to hold:
  1. \(g\) is defined at \(x\text{;}\)
    🔗
    🔗
  2. \(f\) is defined at \(g(x)\text{.}\)
    🔗
    🔗
Thus the implied domain \(D\) of \(f\circ g\) is the set of \(x\in \R\) for which both \(g(x)\) and \(f(g(x))\) are defined. Using set intersection notation (see Definition 1.1.17), we have
\begin{equation*} D=\{x\in \R \mid g \text{ defined at } x\}\cap \{x\in \R \mid f \text{ defined at } g(x)\}\text{.} \end{equation*}
Let’s compute some simple examples. After we develop techniques for solving inequalities, we will consider more complicated examples.
🔗

Example 1.7.13. Composition: implied domain.

Let \(f(x)=1/x\) and \(g(x)=\sqrt{x+1}\text{.}\) Find the implied domain of \(f\circ g\text{.}\)
🔗
Solution.
The implied domain of \(f\circ g\) is the set of \(x\) where \(g(x)=\sqrt{x+1}\) is defined and where \(f(g(x))=1/\sqrt{x+1}\) is defined.
🔗
For \(g(x)=\sqrt{x+1}\) to be defined, we need \(x+1\geq 0\text{,}\) or equivalently \(x\geq -1\text{.}\)
🔗
For \(f(g(x))=1/\sqrt{x+1}\) to be defined, we need further that \(\sqrt{x+1}\ne 0\text{,}\) or equivalently, \(x\ne -1\text{.}\)
🔗
Thus both conditions are satisfied if and only if \(x\in [-1,\infty)\) and \(x\ne -1\text{.}\) In other words, the implied domain of \(f\circ g\) is \((-1,\infty)\text{.}\)
🔗
🔗
🔗

Example 1.7.14. Composition: implied domain.

Let \(f(x)=x^2-1\) and \(g(x)=3x-\tfrac{4}{x}\text{.}\)
  1. Find the implied domain of \(f\circ g\text{.}\)
    🔗
    🔗
  2. Find the implied domain of \(g\circ f\text{.}\)
    🔗
    🔗
🔗
Solution.
  1. The function \(g\) is defined for all \(x\ne 0\text{.}\) Since \(f\) is defined everywhere, there is not further constraint. Thus the implied domain is
    \begin{equation*} \{x\in \R\mid x\ne 0\}\text{.} \end{equation*}
    🔗
    🔗
  2. For \(g\circ f\) to be defined at \(x\) we need \(f\) to be defined at \(x\) and \(g\) to be defined at \(f(x)\text{.}\) As mentioned above, \(f\) is defined everywhere, so the first condition creates no restriction. Since \(g\) is defined only when the input is nonzero, we need \(f(x)\ne 0\) for \(g\) to be defined at \(f(x)\text{.}\) The usual algebra shows that \(f(x)=0\) if and only if \(x=\pm 1\text{.}\) We conclude that the domain of \(g\circ f\) is
    \begin{equation*} \{x\in \R\mid x\ne \pm 1\}=(-\infty, -1)\cup (-1,1)\cup (1,\infty)\text{.} \end{equation*}
    🔗
    🔗
🔗
🔗
🔗

Warning 1.7.15. Composition: implied domain.

When computing the formula for a composition \(f\circ g\text{,}\) there is always the danger of overlooking what the implied domain is. Consider the example where we take \(f(x)=g(x)=1/x\text{.}\) Our usual implied domain analysis yields that the implied domain of \(h=f\circ g\) is the set of all \(x\ne 0\text{.}\) However, if computing a formula for \(h\text{,}\) we see that
\begin{align*} h(x) \amp =f(g(x))\\ \amp =f(1/x)\\ \amp =1/(1/x))\\ \amp = x\text{,} \end{align*}
suggesting that the implied domain of \(h=f\circ g\) should be \(\R\text{.}\) How do we reconcile these two different conclusions? Here’s how: the steps in the algebra above used to compute the formula for \(h\) are only valid for inputs \(x\) where \(f\) and \(g\) are defined in the first place! In other words, our identity \(h(x)=x\) is itself only true for \(x\ne 0\text{,}\) and this is consistent with our determination of the implied domain.
🔗
🔗
🔗
🔗
PrevTopNext